Force and Torque of a Clockwise Current Loop in Magnetic Field

[stunner5000pt]

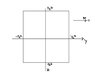
A rectangularl oop carring a clockwise current i is placed in a constant magnetic field B = By. The four corners of the loop are at (x=0, y = +/- a/2, z=+/-b/2 where a and b are positve onstants
find the force and torque, magnitude and direction on each of the four straight lin segments of the loop. Illustrate this device and your answers using a diagram.
force only acts on the vertical (according to the diagram) and points out from the page for y = a/2. For y = -a/2, the force points into th page.
for its magnitude
F = 2 i a B / 2 = i a B Since theta is 90 degrees. B is constant.
the torque points downward in the negative z direction
t=2 (b x F)/2 = b x F = iabB
am i right?

 

[Doc Al]

You mixed up your a's and b's in calculating the force. (The length of the vertical segments is "b", not "a".) Other than that, it looks OK.