Eitan Levy
- 259
- 11
- Homework Statement
- In a system as described in the picture, what would be the force that the infinite wire with a current of i exerts on the wire BC?
- Relevant Equations
- F=BILsinΘ
μThe magnetic field is supposed to be B=μ0i/(2πr). I think that the force would be aimed upwards.
Now I tried to divide the wire BC to infinite smaller wires where B is roughly constant in each one of them.
What I get is:
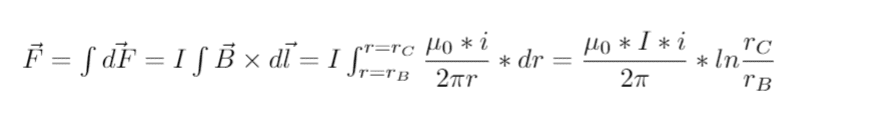
However this is not correct when I plug the relevant numbers in it.
Where is my mistake?
Now I tried to divide the wire BC to infinite smaller wires where B is roughly constant in each one of them.
What I get is:
However this is not correct when I plug the relevant numbers in it.
Where is my mistake?
