Force on submerged plate perpendicular to flow

[tjosan]

Hey,

I wonder how I can calculate the force of a plate that is submerged in water.

I thought maybe the drag equation would be suitable for this with the drag coefficient set to 1.28 (https://www.grc.nasa.gov/www/k-12/airplane/shaped.html). But is implies the flow is according to the image (bottom part, https://en.wikipedia.org/wiki/Drag_coefficient#Background):

But in my case, I only have a flow under the plate, not on both sides:

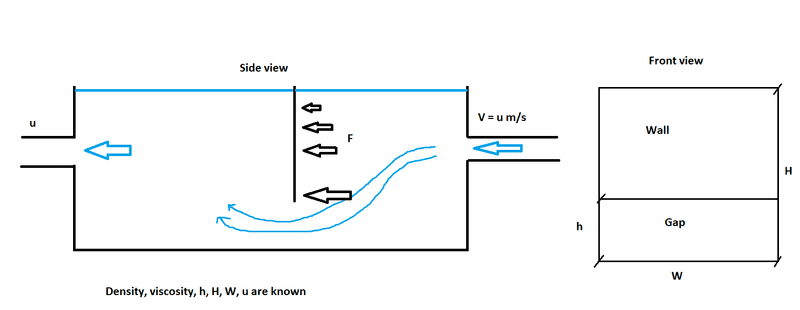
I want to calculate the force at the bottom of the wall. The wall is attached in place. Can anyone assist me how to proceed? Thank you.

 

[Baluncore]

The magnitude of the ram pressure against the plate will be about;
P = ½⋅ρ⋅v² ; pascal.
Where ρ is the density of the water in kg/m³
and v is the water velocity in m/s.

 

[jrmichler]

There is no good way to calculate the force on the plate working from dimensions and flow rate. There are ways to make a rough estimate. The post above by @Baluncore is one such way. Another way is to treat the gap under the plate as an orifice, and use Bernoulli's equation. The pressure difference to create the velocity increase under the plate is the pressure on the plate.

Or you can measure the pressure drop. Your diagram appears to show that the water has a free surface. Measure the difference in water height before and after the plate. That height difference multiplied by the water density is the pressure difference across the plate. The pressure difference times the plate area is the total force on the plate.

 

[Baluncore]

I agree with @jrmichler.
There is really no simple way to analyse the typical operation.

However there are a number of conceivable worst case fault situations that would require consideration during the design process. You are building a "trap".

“The body of an animal falls into the trap and blocks the h * w aperture”. Water on the supply side then overflows. Water on the outlet side falls to the height of the outlet, but is then pumped out by the contractor sent to identify and rectify the problem.

First, you can evaluate the pressure on the area of the plate, by considering the plate as part of a static dam wall, with a hydrostatic pressure differential.

But the body rolls along the bottom surface of the trap, until stopped by the bottom edge of the wall. Half the hydrostatic pressure on the body, ( at a depth = H + h/2 ), appears as a force on the bottom lip of the wall. (It is actually a directed vector dependent on the size, in terms of h, of the cylindrical animal model). That mechanical force against the lip, must be added to the pressure force on the plate.