Miguel Guerrero
- 16
- 0
Homework Statement
You are given a choice of two methods of pulling a 2 kg sled for a distance of 7 meters at a constant speed. If the coefficient of friction is 0.1, which method do you select as involving the least amount of pull on your part?
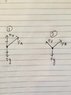
Option 1 is a picture depicting the sled on a horizontally flat surface with the pull being in the direction of 30 degrees above the surface,
Option 2 depicts the sled being pulled up an incline of 30 degrees above the relative horizontal with the pull being in the same direction.
Please help, I determined an answer using correct work, however my instructor insists I am missing a step somewhere.
Homework Equations
Ff=μ*Fn
Fg=m*9.8
Ft=?
The Attempt at a Solution
For option 1, I calculated the force of friction using the coefficient given so that Ff=0.1*(2kg*9.8)=1.96
Using this and the angle of the pull (30 degrees) I drew a triangle for the force that must be applied to move the sled so that cos(30)=1.96/x, x=2.236N applied in the direction of the pull in order to overcome friction. I multiplied this by the 7 meters it needs to travel to get the total work necessary for option 1. W=7*2.236= 15.652
for option 2, I set the axis so that the x-axis was parallel to the table and the y-axis was perpendicular and solved for each component of gravity: Fg-x=19.6sin(30)=9.8 Fg-y=19.6cos(30)=16.974. Again using the coefficient of friction given, I solved for friction by setting the normal force equal to the y-component of gravity so that Ff=0.1*16.974=1.697. I then added this the the x-component of gravity and I multiplied the sum (11.497) by 7 to get the work (80.47)
The problem is that my instructor informed me that there is an error in my work. Something regarding the normal force in option 2 I believe but i can't seem to figure what it is. Please help.