- #1
Thornak
- 2
- 0
Homework Statement
[/B]
This is not a typical homework problem, so I hope I am posting this in the correct place. I am in 12th grade physics and we are dealing with basic kinematics. However, we recently did a set of problems that I did in a way which makes sense and which our textbook (and the rest of the Internet) says is correct, but my physics teacher claimed otherwise. After a little bit of debate, we ended up recreating the situation in class. The results supported my teacher, but I can't believe the rest of the world is wrong. An example problem is below:
Two objects are connected by a massless string and massless/frictionless pulley. m1 weighs 3 kg and hangs off of the table. m2 weighs 5 kg and sits on a frictionless surface. What is the acceleration of m2?
Homework Equations
My way is simple: (m1)*g=(m1+m2)*a, so a=(m1)*g/(m1+m2).
My teacher's way involves drawing free-body diagrams, which you can use in my way and still come to the same answer. However, for the equations of each object, my teacher uses TOTAL mass of the system because "it is all accelerating as one unit." For example, his equation in the y-direction for m1 is Fgravity-Ftension=(m1+m2)*a. And his equation for m2 in the x-direction is Ftension=(m1+m2)*a. When you use these two equations to solve for a, you end up getting Fgravity-(m1+m2)*a=(m1+m2)*a, so a=Fgravity/[2(m1+m2)]=m*a/[2(m1+m2)]. Thus, his answer is always half of mine.
The Attempt at a Solution
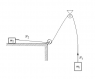
With the entire Internet backing me up, I assumed I was correct. But when we recreated the situation in class, the results supported my teacher's answers. The only difference in our experiment was that obviously the massless, frictionless conditions were not met, though my teacher assured the class that they were negligible (we used light pulleys and a toy car on wheels). Also, the setup was slightly different, as shown below:
(Sorry for the crappy diagram. I quickly cooked this up in MS paint. But I think you get the point.)
I don't believe the two pulleys in this experiment matter because they do not create a pulley system. They simply redirect the force twice instead of once. I may be wrong, though.
My question is twofold: First, who is correct and who is not? And second, if I am technically correct, why did the experiment yield results that supported my teacher's claim? This is an issue that will probably reappear as the year goes on, so I need to figure this out. Thank you!