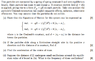Forces on particles and second order DE's

[dawud]

Homework Statement

Attached. If you don't mind I'd like to go through each part of the question to make sure I've understood correctly. Thanks a lot

Homework Equations

F=qE
F=(γq^2)/(d^2)
F=Kx
Taylor/Maclaurin (?)

The Attempt at a Solution

So for part (a) I know that Coulomb's interaction, the spring force, and the electric force all act on the particles, so by adding all these force vectors I will obtain the required vector equations. However, I'm not sure on the directions of the forces; why is the electric force F=qE positive for in both vector equations (do they act in the same direction and if so, which?), and why is the restoring spring force opposite for the each of the two?

As for the other parts, I don't really know where to begin.

 

[BvU]

Electric force $qE$ is pointing the same way for both particles: both have the same charge.
The other electric force $\gamma(q^2/d^2)$ is pointing in a different direction for each particle: both have the same charge, so they repel each other. (Or: E field $\vec E =\gamma(q/d^2)\ \hat r$ of 1$\rightarrow$2 points opposite from 2$\rightarrow$1.
And the spring pulls particles towards each other, so also in opposite directions.

(b) what does d = constant mean for $\ddot x_1-\ddot x_2$?

(c) what is the coordinate of the center of mass ?

(d) write $d = d_{eq} + a \cos{\omega t}$ with $d_{eq}$ from (b)