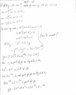Form of a particular solution for N.H.L.D.E. w/ constant coefficients

[jegues]

Homework Statement

You are given that the roots of the auxiliary equation associated with the linear, differential equation

\phi(D)y = 2x- 3xe^{-3x}

are m = \pm2,0,0. Write down the form of a particular solution of the differential equation as predicted by the method of undetermined coefficients. Do NOT find the coefficients, just the form of the particular solution.

Homework Equations

The Attempt at a Solution

See figure attached for my attempt at the solution. I'm not entirely convinced I'm doing this properly so I'd just like for someone to verify my work.

Thanks again!

 

[LCKurtz]

Not sure what the various rules you refer to are, but the answer and reasoning look right to me.