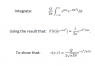- #1
binbagsss
- 1,254
- 11
Problem
F denotes a forward Fourier transform, the variables I'm transforming between are x and k
- See attachment
Relevant equations
So first of all I note I am given a result for a forward Fourier transform and need to use it for the inverse one.
The result I am given to use, written out is :
## \int e^{-ikx} e^{-\alpha x^{2}} dx = \frac{1}{2\alpha} e^{-k^{2}/4\alpha} ##
I note that ## F(k) C(t) ## gives me a function of k, so I apply ## F^{-1} ## on this I get a function of x.
Attempt:
My thoughts are I'm looking to change signs in my exponential terms so that it is , effectively a forward transform and then use the result, so just thinking of it as a integration result rather than a particular Fourier transform.However if I do this my exponential terms are:## e^{-(-ikx+\alpha k^{2})} ##
, I don't know how I can then apply the result, completing the square looks like the only candidate to me , but this seems like it will be too scrappy, in particular with 'i' terms, how do I deal with this ## e^{ikx} ## term, if I'm on the right lines, is completion of the square necessary or is there some other approach to being able to use this result ?Many thanks in advance.
F denotes a forward Fourier transform, the variables I'm transforming between are x and k
- See attachment
Relevant equations
So first of all I note I am given a result for a forward Fourier transform and need to use it for the inverse one.
The result I am given to use, written out is :
## \int e^{-ikx} e^{-\alpha x^{2}} dx = \frac{1}{2\alpha} e^{-k^{2}/4\alpha} ##
I note that ## F(k) C(t) ## gives me a function of k, so I apply ## F^{-1} ## on this I get a function of x.
Attempt:
My thoughts are I'm looking to change signs in my exponential terms so that it is , effectively a forward transform and then use the result, so just thinking of it as a integration result rather than a particular Fourier transform.However if I do this my exponential terms are:## e^{-(-ikx+\alpha k^{2})} ##
, I don't know how I can then apply the result, completing the square looks like the only candidate to me , but this seems like it will be too scrappy, in particular with 'i' terms, how do I deal with this ## e^{ikx} ## term, if I'm on the right lines, is completion of the square necessary or is there some other approach to being able to use this result ?Many thanks in advance.