Fourier transformation for circular apertures

[QuarkDecay]

Homework Statement

Find the Resolution of a circular aperture with a radius of a

Relevant Equations

Fourier transformations noted below

My notes say that the Resolution of the Aperture(in the Electric field of the wave) is the Fourier transformation of the aperture.
Then gives us the equation of the aperture:

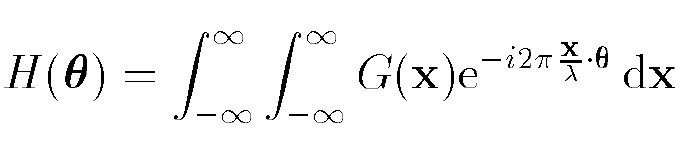
and says that for the circular aperture in particular also:

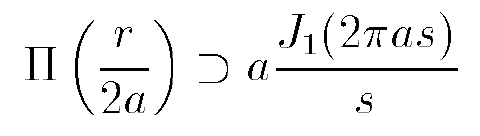
My attempt at solving this:

We know that the Fourier transformation in general is :

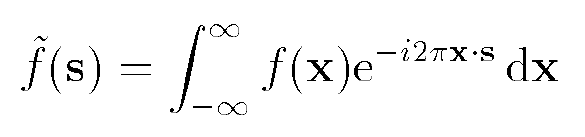
For circular aperture we have G(x)=Π(r/2a). So I thought that if I manage to turn the θ/λ inside the H(θ) equation into an s, (θ/λ=s or θ=λs), then I could say G(x)=Π(r/2a) ⊃ aJ₁(2πas)/s, therefore H(θ)= aJ₁(2πas)/s, but not this one exactly, because I need to change the s inside the H(θ) equation.

So H(θ=λs)=∫∫G(x)e^-i2πsxdx
But now we have an H(λs) instead of an H(θ), so we need to use this Fourier property

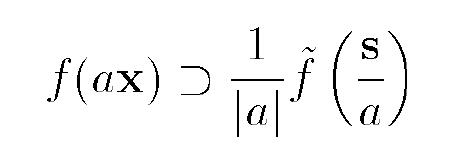
and this is where I stop because I don't know which is which, and I don't know how this ⊃ works much.
I tried replacing the s with s=θ/λ and say
H(λ*θ/λ)=Η(θ)=aJ₁(2πa(θ/λ))/(θ/λ) But I always get a result of
H(θ)=DλJ₁(πDθ/λ)/(2θ) and the result is supposed to be this:

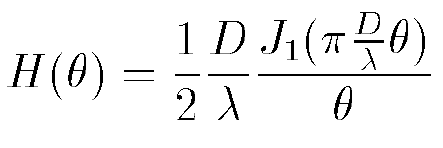
I always get the λ on the top. And again, when I tried using the

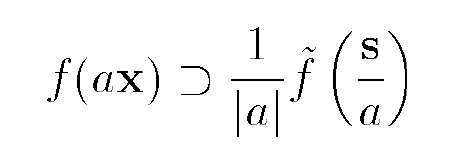
I still got the same result, although I'm not sure if I'm appliying this to the H(λs) right, but the book does say that I need to use the property above somewhere.
My main problem is that I can't really solve Fourier transformation and don't understand very well how this ⊃ symbol works

 

[pasmith]

I've no idea what $\supset$ is supposed to mean in this context.

Start from $$H(\boldsymbol{\theta}) = \iint_{\mathbb{R}^2} G(\mathbf{x}) e^{-2\pi i \boldsymbol{\theta} \cdot \mathbf{x}}\,dA$$ where so far as I can tell from googling the aperture function $G(\mathbf{x})$ is equal to 1 if $\|\mathbf{x}\| \leq a$ and 0 otherwise. By symmetry we can orient the coordinate axes such that $\boldsymbol{\theta} = (0,\theta)$. Now change to plane polar coordinates $(r, \phi)$ to obtain $$H(\mathbf{\theta}) = \int_0^a r \int_{-\pi}^{\pi} e^{-2\pi i r \theta \sin \phi / \lambda}\,d\phi\,dr.$$ The integral over $\phi$ can be done by making use of the integral representation $$J_0(z) = \frac 1{2\pi} \int_{-\pi}^{\pi} e^{-iz\sin\phi}\,d\phi$$ and the resulting integral over $r$ can be done by substitution, noting that $$\frac{d}{dz} (zJ_1(z)) = zJ_0(z).$$

 

[QuarkDecay]

I've no idea what $\supset$ is supposed to mean in this context.

Start from $$H(\boldsymbol{\theta}) = \iint_{\mathbb{R}^2} G(\mathbf{x}) e^{-2\pi i \boldsymbol{\theta} \cdot \mathbf{x}}\,dA$$ where so far as I can tell from googling the aperture function $G(\mathbf{x})$ is equal to 1 if $\|\mathbf{x}\| \leq a$ and 0 otherwise. By symmetry we can orient the coordinate axes such that $\boldsymbol{\theta} = (0,\theta)$. Now change to plane polar coordinates $(r, \phi)$ to obtain $$H(\mathbf{\theta}) = \int_0^a r \int_{-\pi}^{\pi} e^{-2\pi i r \theta \sin \phi / \lambda}\,d\phi\,dr.$$ The integral over $\phi$ can be done by making use of the integral representation $$J_0(z) = \frac 1{2\pi} \int_{-\pi}^{\pi} e^{-iz\sin\phi}\,d\phi$$ and the resulting integral over $r$ can be done by substitution, noting that $$\frac{d}{dz} (zJ_1(z)) = zJ_0(z).$$

Thanks a lot...! I'm quite desperate over this problem and I couldn't find the solution anywhere over the web. Been searching for it for three days. Now I hope I can solve the rest of it lol