nubshat
- 6
- 0
A hand supports two books, ma and mb, with ma on top. The hand accelerates the books p and to the right, with a pushing force directed 64° above horizontal. Assuming the upper book does not slip, draw a free body diagram for each book.
My attempt:
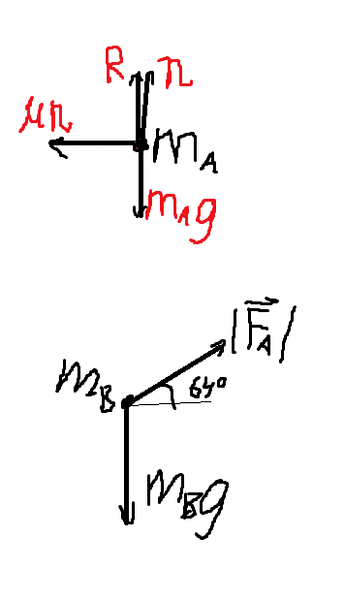
My attempt: