cooldudeachyut
- 5
- 0
Homework Statement
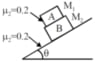
Two block M1 and M2 rest upon each other on an inclined plane. Coefficient of friction between surfaces are shown. If the angle θ is slowly increased, and M1<M2 then
Options :
1- Block A slips first.
2- Block B slips first.
3- Both slip simultaneously.
4- Both remain at rest.
Homework Equations
Taking frictional force between the two blocks as f1 and between the block B and inclined plane as f2, the equations for limiting values f1max and f2max :
f1max = μ2M1gcosθ
f2max = μ2(M2+M1)gcosθ
The Attempt at a Solution
For Block A :
I only considered the case where f1 reaches its limiting value, hence I get this inequality as the condition when block A may start slipping,
M1gsinθ - μ2M1gcosθ ≥ 0
Which is equivalent to,
tanθ ≥ μ2
For Block B :
Again, I only considered the case where f2 reaches its limiting value but cannot figure out what's the magnitude/direction of f1 on this block. So I assumed f1max to act on this block in the direction up the slope as this basically provides least resistance and also complies with block A's case which may as well be the "limiting factor" for the case where block B slips, giving my inequality as,
M2gsinθ - μ2(M2+M1)gcosθ + μ2M1gcosθ ≥ 0
Which is again equivalent to,
tanθ ≥ μ2
I'm confused how to proceed now as I think both blocks should start slipping simultaneously however the answer provided is option 2, i.e., block B will slip first.