chopnhack
- 53
- 3
Member advised to use the homework template for posts in the homework sections of PF.
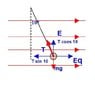
This is a general question about tension in a string. If we have a string that makes an angle theta of 10 degrees with the vertical, what would the tension in the string be.
If we assume a mass of 0.025kg at the end of 0.8m long string, I calculate that the force acting opposite mass x gravity would be Tcos10degrees. If we rewrite this to solve for T = 0.245N/cos 10
My question comes from an observation, as we take values of higher angles, nearly horizontal for instance, cos 89 (perpendicular to the vertical axis) = 0.01745. If we divide 0.245N by this value we get a number much larger than the original when tension should be nearly zero.
The picture is from the solution to the example where the thought arose from.
If we assume a mass of 0.025kg at the end of 0.8m long string, I calculate that the force acting opposite mass x gravity would be Tcos10degrees. If we rewrite this to solve for T = 0.245N/cos 10
My question comes from an observation, as we take values of higher angles, nearly horizontal for instance, cos 89 (perpendicular to the vertical axis) = 0.01745. If we divide 0.245N by this value we get a number much larger than the original when tension should be nearly zero.
The picture is from the solution to the example where the thought arose from.
Attachments
Last edited: