Gauss's Law: An line of charge and a sphere, find flux

[Breedlove]

Homework Statement

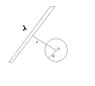
An infinitely long line charge having a uniform charge per unit length $$\lambda$$ lies a distance d from point O as shown. Determine the total electric flux through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases, where R<d and R>d

Homework Equations

$$\Phi$$=$$\stackrel{Q}{\epsilon}$$
$$\lambda$$=Q/L
$$\Phi$$=$$\int$$E(dot)dA

The Attempt at a Solution

So I know that when R<d that the flux is zero because there isn't a charge enclosed. Howevever, when R>d the charge that is in the sphere gives off an electric field which is not going to be constant through the sphere. Isn't the magnitude of the electric field going to be different as the distance to different parts of the sphere is varied? Because of this, saying $$\stackrel{Q}{\epsilon}$$ = $$\int$$E(dot)dA isn't going to help because E can't be taken out of the integral. (dA representing the vector of a small piece of the area of the sphere centered around point O)

So I was thinking if we made a gaussian cylinder around the line of charge and made it so that the cylinder engulfs the point O. Would that be right? That approach really wouldn't be answering the question posed in the problem, but I'm pretty sure that I can't really do anything with O.

Am I wrong in my statement that there isn't sufficient symmetry to take E out of the integral?

I'm thinking that the amount Qenclosed is going to be some sort of function of R. Is that the way to go? All I need to find is flux, so messing about with E may be a waste of time?

Thanks for your help with this!

Tell me how the picture downloads, it's my first time doing that, I hope it works!

 

[rl.bhat]

I'm thinking that the amount Qenclosed is going to be some sort of function of R. Is that the way to go?

When the R>d, find the length of the line of charge inside the sphere by using geometry.
Applying the Gauss's law to find the total elecgtric flux through the sphere.

 

[Breedlove]

What kind of geometry? Are there any clues you can give me to help me find the length of the line of charge inside the sphere?

 

[rl.bhat]

Draw a sphere with a line intersecting it. Draw a perpendicular on the line from the center. This will be the distance d of the line from the center. Draw a triangle with extreme points on the line and the center. Now try to find the length of the line.