Shaun97
- 5
- 0
I can't seem to find the proof for the distance between the two parallel lines.
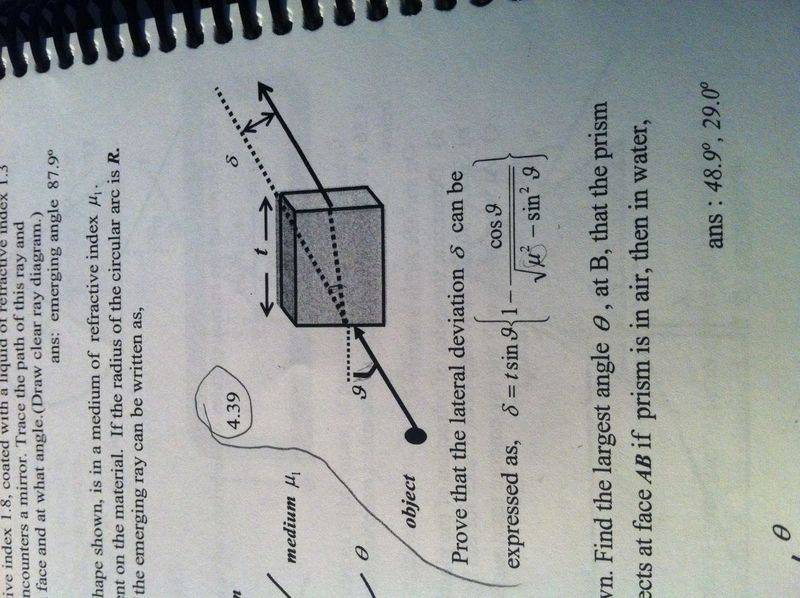
Sin (A+B)= sinAcosB + sinBcosA[/B]
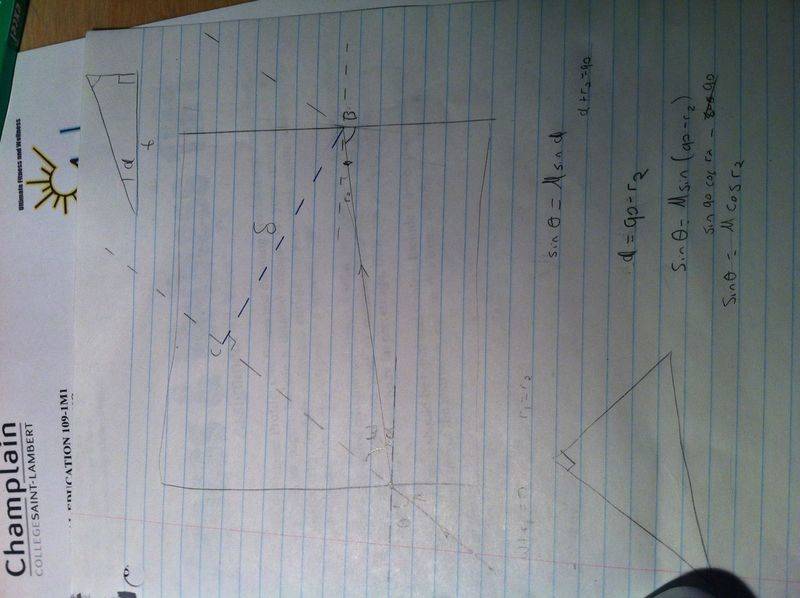 [/B]
[/B]
Homework Equations
: Snells law: μ1sinθ1=μ2sinθ2Sin (A+B)= sinAcosB + sinBcosA[/B]