aatari
- 73
- 3
Hi Fellas could someone kindly check my solution, please.
Calculate the force of gravity between you and your computer monitor. Estimate suitable values. (Women: 40 kg to 60 kg, men: 50 kg to 80 kg). Why have you not noticed this force?
Fg = m1xm2/d2[/B]
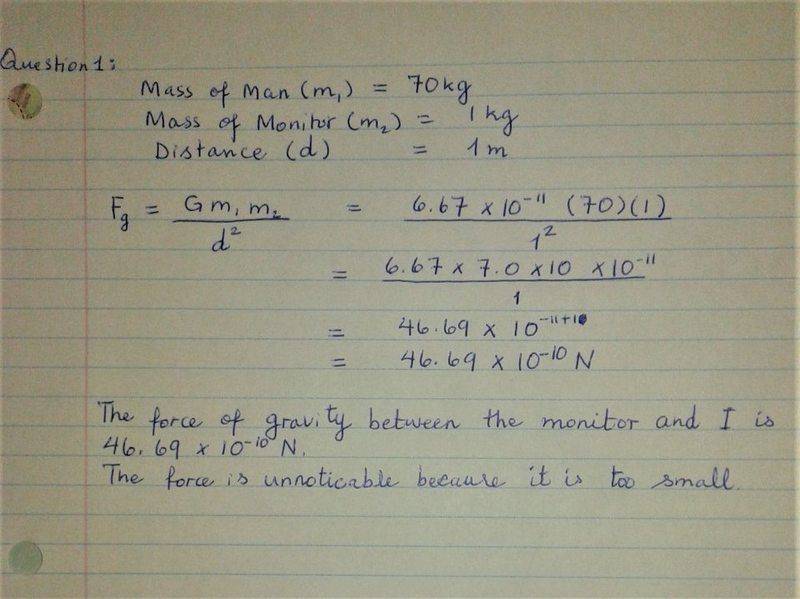 [/B]
[/B]
Homework Statement
Calculate the force of gravity between you and your computer monitor. Estimate suitable values. (Women: 40 kg to 60 kg, men: 50 kg to 80 kg). Why have you not noticed this force?
Homework Equations
Fg = m1xm2/d2[/B]