i_hate_math
- 150
- 2
Homework Statement
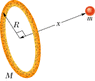
Several planets (Jupiter, Saturn, Uranus) are encircled by rings, perhaps composed of material that failed to form a satellite. In addition, many galaxies contain ring-like structures. Consider a homogeneous thin ring of mass 2.1 x 1022 kg and outer radius 4.3 x 108 m (the figure). (a) What gravitational attraction does it exert on a particle of mass 76 kg located on the ring's central axis a distance 4.5 x 108 m from the ring center? (b) Suppose that, starting at that point, the particle falls from rest as a result of the attraction of the ring of matter. What is the speed with which it passes through the center of the ring?
Homework Equations
Kepler's 3rd Law: T^2=(4*π^2/GM)*R^3
F=GmM/R^2
The Attempt at a Solution
I haven't really been able to attempt this question, I have absolutely no idea how to establish a relation between the mass on the axis and the ring. Please enlighten me with your genius ideas!