GRE question - angular momentum

[eprparadox]

Homework Statement

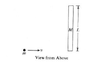
A uniform stick of length L and mass M lies on a frictionless horizontal surface. A point particle of mass m approaches the stick with speed v on a straight line perpendicular to the stick that intersects the stick at one end as shown in the attached image. After the collision, which is elastic, the particle is at rest. What is the speed, V, of the center of mass of the stick after the collision.

a) (m/M)*v
b) m/(m+M)*v
c) sqrt(m/M)*v
d) sqrt(m/(m+M))*v
e) (3m/M)*v

Homework Equations

Ki = Kf
Li = Lf = I*w = mvr
Pi = Pf

The Attempt at a Solution

So I've solved this problem using linear momentum. I said mv = MV. and I get V = (m/M)*v. This is the correct answer. (choice a)

But I cannot for the life of me, solve this using angular momentum and I was hoping I could get some help with that.

First, using angular momentum:
I said that right before the collision the the angular momentum of the particle is mv(L/2) (relative to the center of mass of the stick). Then after the collision, the angular momentum of the center of mass is I*w.

I initially set those two expressions equal to one another and solve but that doesn't give me the correct answer.

I think I'm leaving out a term, but I don't know what it is or how to find it.

Thank you very much!

 

[anathema]

Thank you for your question. Solving this problem using angular momentum can be a bit trickier, but I can guide you through the steps.

First, let's define our coordinate system. We can take the origin at the point where the particle collides with the stick, and the positive x-direction pointing towards the rest of the stick. This means that the initial angular momentum of the particle is given by L = mvr, where r is the distance from the origin to the point where the particle collides with the stick.

Next, let's consider the angular momentum of the stick about its center of mass. Since the stick is initially at rest, its initial angular momentum is zero. After the collision, the stick will start rotating about its center of mass with an angular velocity w. Using the parallel axis theorem, we can write the final angular momentum of the stick as L = I*w + M*V*r, where I is the moment of inertia of the stick about its center of mass and V is the velocity of the center of mass.

Now, we can equate the initial and final angular momentum and solve for V. This gives us:

mvr = I*w + M*V*r

Since the collision is elastic, we know that the total kinetic energy before and after the collision are equal. This means that we can also write the initial and final kinetic energies as:

1/2*m*v^2 = 1/2*I*w^2 + 1/2*M*V^2

We can use the parallel axis theorem again to express the moment of inertia I in terms of the moment of inertia about the center of mass Icm and the distance from the center of mass to the point where the particle collides r:

I = Icm + M*r^2

Substituting this into the equation for kinetic energy, we get:

1/2*m*v^2 = 1/2*(Icm + M*r^2)*w^2 + 1/2*M*V^2

Now, we can solve for V in terms of v and other known quantities:

V = sqrt((m*r^2*v^2)/(Icm + M*r^2))

To simplify this expression, we can use the parallel axis theorem once more to express the moment of inertia Icm in terms of the total moment of inertia I and the distance between the point where the particle collides and the center of mass

 

[tomcue]

The correct answer using angular momentum would be choice d) sqrt(m/(m+M))*v. To solve this using angular momentum, we need to consider the angular momentum of the system before and after the collision.

Before the collision, the angular momentum of the system is given by mvr, where v is the velocity of the particle and r is the distance from the particle to the center of mass of the stick. This can also be written as m(L/2)v, since the particle is approaching the stick at a distance of L/2 from the center of mass.

After the collision, the angular momentum of the system is given by Iw, where I is the moment of inertia of the stick and w is the angular velocity of the stick. We can calculate the moment of inertia of the stick using the parallel axis theorem, which states that I = Icm + md^2, where Icm is the moment of inertia about the center of mass and d is the distance from the center of mass to the point of collision. In this case, d = L/2, so I = Icm + mL^2/4.

Now, we can set the two expressions for angular momentum equal to each other and solve for w:

m(L/2)v = (Icm + mL^2/4)w

w = (m(L/2)v) / (Icm + mL^2/4)

Since the particle comes to rest after the collision, the final angular velocity of the stick must be equal to the initial angular velocity of the particle. Therefore, we can set w equal to v/r, where r is the distance from the center of mass of the stick to the point of collision. In this case, r = L/2, so we have:

v/r = (m(L/2)v) / (Icm + mL^2/4)

Solving for v, we get:

v = sqrt(m/(m+M)) * v

Therefore, the correct answer using angular momentum is choice d) sqrt(m/(m+M))*v.