- #1
VVS2000
- 150
- 17
so I was studying H theorem from Richard Fitzpartic's site.
https://farside.ph.utexas.edu/teaching/plasma/Plasma/node35.html
Given H,
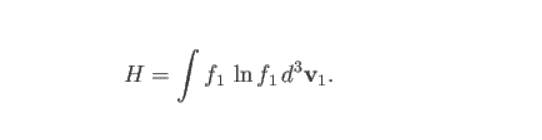
they consider the following equation

and set the constants as
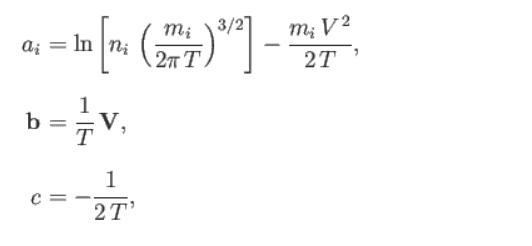
I want to understand how they got these particular values for a, b &c
can we consider the following as constraints and a b c as lagrange multipliers and solve for them?
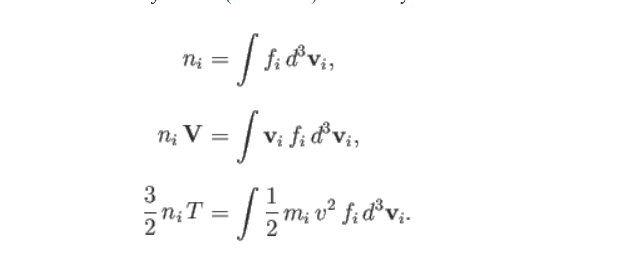
or if there are any other ways to obtain a b c plz do tell
thanks in advance
https://farside.ph.utexas.edu/teaching/plasma/Plasma/node35.html
Given H,
they consider the following equation
and set the constants as
I want to understand how they got these particular values for a, b &c
can we consider the following as constraints and a b c as lagrange multipliers and solve for them?
or if there are any other ways to obtain a b c plz do tell
thanks in advance