Karma
- 76
- 0
Hard Vector Question Much Help Needed!
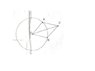
Points A and B are any two points on a cirlce with a center O. The heads of Vectors OA and OB lie on the circle. Vector OC is the sum of OA and OB . In the Diagram, the head of OC lies outside the circle. Explain your answer to each question.
a.)Is it Possible for the head of OC to lie on the Circle?
b.)Is it Possible for the head of OC to lie inside the circle?
c.)Where are all the possible positions for C?
Here is the Diagram! Thank you any help is appreciated. I tried doing some of the questions but All my answers were wrong, and i got confused, please help me! thank you very much
Points A and B are any two points on a cirlce with a center O. The heads of Vectors OA and OB lie on the circle. Vector OC is the sum of OA and OB . In the Diagram, the head of OC lies outside the circle. Explain your answer to each question.
a.)Is it Possible for the head of OC to lie on the Circle?
b.)Is it Possible for the head of OC to lie inside the circle?
c.)Where are all the possible positions for C?
Here is the Diagram! Thank you any help is appreciated. I tried doing some of the questions but All my answers were wrong, and i got confused, please help me! thank you very much