Hawking Radiation: Qs re Energy Density at r > Rc

[Buzz Bloom]

In my Part I post
https://www.physicsforums.com/threads/qs-re-hawking-radiation-part-i.873163/reply?quote=5482437
I asked if there were any errors in my summary description of the Hawking radiation phenomenon. So far none have been posted.

In this thread I want to learn some additional facts about the phenomenon. Can someone please tell me, in terms of the Schwartzchild metric, what the BH energy density is of the gravitational field at radius
r > R_c.

I am guessing that this energy density is functionally related to the scalar curvature at r. I found the following formula for this scalar at
http://www.physicspages.com/2014/03/16/riemann-tensor-in-the-schwarzschild-metric/ .

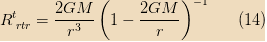
I think that this form assumes c = 1. Therefore 2GM = R_c, and the scalar can then be written as:
(R_c/r³) × ( 1 - R_c/r)^-1

In SI units this scalar has the units m^-2. Therefore, I assume that it is not the curvature, but the rather the curvature squared, and the actual curvature scalar is equal to the squareroot of this expression.

If my guess is correct, what is the functional relation between the curvature and the gravitational field energy density?

 

[phyzguy]

There is no unambiguous description of the energy density of the gravitational field. This has to do with the fact that it is impossible to localize the energy density of a gravitational field, because one can always choose a coordinate system which is locally flat, even in a curved spacetime. I would refer you to two references:

(1) Landau, Lifshitz, "The Classical Theory of Fields", Section 101, "The Energy-Momentum Pseudotensor". This is about the best that can be done to describe the energy density of the gravitational field.

(2) Misner, Thorne, Wheeler, "Gravitation", Section 20.4 "Why the energy of the gravitational field cannot be localized". An excellent description of the attempts that have been made to answer your question.

 

[Buzz Bloom]

This has to do with the fact that it is impossible to localize the energy density of a gravitational field, because one can always choose a coordinate system which is locally flat, even in a curved spacetime.

Hi @phyzguy:

Thank you for your post. I recall reading in MTW a description about why the total amount of mass with uniform density in a finite universe is not definable. I found the explanation to be be incomplete, but in a subsequent discussion on the PF I have learned that this limitation is related to the impossibility of including the mass equivalent of binding energy. I intend to look up your LL citation, but it is likely to take me at least several weeks.

I am unclear about what the word "localize" means in this context. What I would like to find out is the gravitational energy dE in the volume dV of a spherical shell, at radius r > R_s from the BH center, with thickness dr. I am not confident I understand this well, but I think with respect to the Schwartzchild metric

dV = 4π r² (1 - R_s/r)^-1/2 dr.​

Is a volume such as dV localized?

Regards,
Buzz

 

[Buzz Bloom]

Hi @phyzguy:

The reason I am seeking the GF energy density is because I am guessing that the probability distribution of a particle pair, within a specified range of mass and momentum, being created from the GF energy in dV at radius r depends on the GF energy density in this dV volume. Is this correct?

Regards,
Buzz

 

[pervect]

Regardless of the reason WHY you're interested in something that doesn't exist (in this case the notion of energy density of the gravitational field) - it still doesn't exist :(.

The issue has been known about for a long time. As early as 1918, three years after the discovery of GR in 1915, Hilbert was writing about "the failure of the energy theorem". Rather than get directly into the technical aspects, I'll give a bit of the history, from https://arxiv.org/abs/physics/9807044 .

Though the general theory of relativity was completed in 1915, there remained unresolved problems. In particular, the principle of local energy conservation was a vexing issue. In the general theory, energy is not conserved locally as it is in classical field theories - Newtonian gravity, electromagnetism, hydrodynamics, etc.. Energy conservation in the general theory has been perplexing many people for decades. In the early days, Hilbert wrote about this problem as ‘the failure of the energy theorem ’. In a correspondence with Klein [3] he asserted that this ‘failure’ is a characteristic feature of the general theory, and that instead of ‘proper energy theorems’ one had ‘improper energy theorems’ in such a theory. This conjecture was clarified, quantified and proved correct by Emmy Noether.

The above paper does a good job of talking about the history, but the way it explains the difficulty is a bit awkwards in modern terminology. For a modern and non-technical overview of the issue, I'd recommend the Sci.physics.faq", which I'll link to and briefly quote.

http://math.ucr.edu/home/baez/physics/Relativity/GR/energy_gr.html

Is Energy Conserved in General Relativity?

In special cases, yes. In general — it depends on what you mean by "energy", and what you mean by "conserved".

In flat spacetime (the backdrop for special relativity) you can phrase energy conservation in two ways: as a differential equation, or as an equation involving integrals (gory details below). The two formulations are mathematically equivalent. But when you try to generalize this to curved spacetimes (the arena for general relativity) this equivalence breaks down. The differential form extends with nary a hiccup; not so the integral form.

Noether's theorem is still regarded by many (perhaps not all) as a key insight into the issue of when energy is conserved and why. In special cases, there are known ways of getting around Noether's theorem that are applicable to GR - for instance, if an asymptotically flat space-time exists, there are well-defined notions of energy such as the Bondi energy and the ADM energy. Additionally, the existence of timelike Killing vectors gives rise to the important Komar energy.

 

[Vanadium 50]

I asked if there were any errors in my summary description of the Hawking radiation phenomenon. So far none have been posted.

That doesn't mean there are any. People might, for example, find your posting style of a parade of incorrect statements frustrating and not worth their time to reply. Or they might find that your habit of posting these same incorrect statements on Wikipedia and blaming this on PF infuriating and not want to get involved. One needs to be careful about the conclusions drawn.

 

[Buzz Bloom]

(in this case the notion of energy density of the gravitational field) - it still doesn't exist :(.

Hi @pervect:

If I understand you comment correctly, you are saying that although the gravitational field surrounding a black hole has energy, and that this energy is the source of Hawking Radiation, the concept that this energy has a density is wrong. That is, this energy of the gravitational field doesn't have any density. Is my understanding correct?

Regards,
Buzz

 

[Buzz Bloom]

That doesn't mean there are any. People might, for example, find your posting style of a parade of incorrect statements frustrating and not worth their time to reply. Or they might find that your habit of posting these same incorrect statements on Wikipedia and blaming this on PF infuriating and not want to get involved. One needs to be careful about the conclusions drawn.

Hi @Vanadium 50:

I know that that the absence of posts showing me my errors does not mean there are no errors. I get the impression that my mentioning of the absence has some how offended you. Perhaps it is my style of writing. If so I apologize.

You say that my summary is "a parade of incorrect statements". I would much appreciate it if you would point out to me one specific error.

Regarding your reference about my posting "these same incorrect statement on Wikipedia", I have no idea what you are referring to. I have made no posts to Wikipedia on this topic. It is true that I have been chastised here on the PF about a previous post to Wikipedia, but I don't see any connection that event has with the current discussion.

Regards,
Buzz

 

[PeterDonis]

I would much appreciate it if you would point out to me one specific error.

Pretty much the whole post is in error. But if you want a few specific items, see the post I just made in that thread.

 

[PeterDonis]

As for this thread, since it is based on the same incorrect premises as the OP's previous one, it is closed.