Heat Flow in Three Identical Rods of Metal

[zorro]

Homework Statement

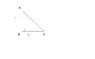
Three rods of identical cross-sectional area are made from the same metal, form the sides of an isosceles triangle ABC right angled at B. The points A and B are maintained at temperature T and √2 T respectively in steady state. Assume that only heat conduction takes place. Then

a) Rate of heat flow in BA is equal to rate of heat flow in CA

b) Temperature gradient across CA is equal to the temperature gradient across BA

The Attempt at a Solution

I got the temperature at C as 3T/1+√2.

Temperature at B > Temperature at A.
Rate of flow in BA will be equal to the rate of heat flow in BCA (not CA)
Again temperature gradient will be same across BCA

Both a and b are correct. I don't understand how. Help.

 

[AC130Nav]

Homework Statement

Three rods of identical cross-sectional area are made from the same metal, form the sides of an isosceles triangle ABC right angled at B.

How can isosceles triangle ABC be right angled at B?

 

[rl.bhat]

Your calculation of temperature at C is wrong.
The two statements are true for BA and BC, rather BA and CA.
Check the problem.

 

[zorro]

How can isosceles triangle ABC be right angled at B?

Take a look at the figure.

Your calculation of temperature at C is wrong.

I found the temperature at C by equating the rate of heat flow through BC and CA.
I got the same answer after checking.