Amith2006
- 416
- 2
Sir,
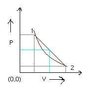
A volume V and pressure P diagram was obtained from state 1 to state 2 when a given mass of a gas is subjected to temperature changes. Based on this graph it is interpreted that, the gas is heated in the beginning and cooled towards the end. Can you please explain this?
A volume V and pressure P diagram was obtained from state 1 to state 2 when a given mass of a gas is subjected to temperature changes. Based on this graph it is interpreted that, the gas is heated in the beginning and cooled towards the end. Can you please explain this?