Post #26:
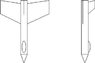
1. I agree. Here's another picture, a continuation from the post#22 picture, with the origin shifted to where you have it too.
A. Coming down along a straight line with constant speed. 1mg downward force from the gravitational field of the Earth is counteracted by the pilot's restraining belts. The pilot experiences 1g downwards (for him: forward, towards the nose of the plane, towards the earth) but doesn't accelerate because the forces executed by the belts hold him at the speed of the plane. This is what we call the normal force in static cases: eg. pilot's weight on chair in office: force mg down, equal but opposite normal force up: zero sum, no motion. What you feel in such situation is called 1g. In the picture: 'felt' 1g down, 'felt' acceleration: red Arrow, size g, up. This is present constantly throughout the entire flight of the plane.
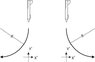
B. The moment he pulls the stick and the plane executes the command, he starts to describe a circle. The OP wording and our state of knowledge about kinematics kind of dictate that the plane's trajectory is a quarter part of a circle. Required centripetal force: 4 mg (value to be justified later) towards center, so at point B that is in positive x direction. Required acceleration: 4g in positive x direction. In addition to that, the 1g from before still applies.(What is an SHM model?). Acceleration 4g in positive x direction plus 1g in positive y direction add up to the purple vector sum. Dotted lines: this is how you add vectors, with a parallellogram. Magnitude of the actual acceleration: √17 g. The pilot experiences this √ 17 g in exactly the opposite direction: he was already leaning in his belts (1g), now he's also pushed into his chair (4g).
C. Centripetal force has turned a bit and aligns more with the normal force. Less strain in the belts, more push from the chair.
D. even less belts, more chair
E. Lowest point, just before pilot pushes back the stick to go to level flight. Acceleration to describe circle still 4g, straight up. Acceleration to counteract gravity and NOT fall towards the Earth any further 1g, straight up. Two independent effects, combined to add up to the pilot experiencing 5g pushing him down in his seat. Just what he can stand while remaining conscious. Hence the 4g at B.
Still E. Plane is now horizontal and pilot pushes back the stick to go to level flight. Plane obeys instantly. No more circle. Acceleration to counteract gravity and NOT fall towards the Earth 1g, straight up.
F. Level flight. Force to counteract gravity 1 mg, delivered by the seat. But the pilot feels 1g down.
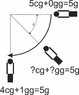
2. It is not 4g down. I used Which was wrong and confusing. My apologies.(*) He feels 1 down, 4 to the left. He is accelerated by an acceleration 1g up (belts) plus 1 g down (gravity) and 4g to the right. That way the net force is towards the center of the circle .
This centripetal force rotates ##+\pi/2## until it is 4mg up. Gravity is still there and needs to be counteracted by another 1mg up. Pilot feels 5g pushing him down in his chair.
(*)I realize I repeated this error by copying to post #35 without checking. Sorry once more. Lot has predictive gifts!
3. For uniform circular motion in the absence of other forces: yes. In this exercise, there is another (constant) force present: Earth gravity.
4. Yes.
5. There is a 1mg force down. But we were told the plane moves at 1200 km/h, a constant speed. Not unreasonable: the air resistance at such speeds is hefty. I would vote for counteracting this 1mg so the trajectory becomes a circle and we can apply our ^v2/r
6. See the apology under 2. I confused you and didn't realize I had done so. Then I made it worse by repeating.
So much on the quote. I'm running behind. What a dilemma: too quick and you confuse people, too slow and a thread becomes a plate of spaghetti. Fortunately we are having good fun.
Lewando throws in the scenarios, very instructive.
Lok wants a more complicated trajectory by using the full 5g as much as he can. I wonder if he would stay conscious when braking at 5g while simultaneously turning up at 5g. My pilot son tells me the braking is worse because you have the sensation of falling over forward. Nauseating for sure; don't know about influence on consciousness. Will interrogate him some more on this. Any aeronaut listening in?
Lot also turns to the left. What is it with these guys ;-) Good thing none of us means it in a bad way ;-) (I should brush up my smiley knowledge).
Time for me to turn in. Look forward to negation's next exercise! Good thing he likes big-picture thinking (rockets, space stations, no eart nearby and all that)
This surely has become some kind of knotted cable instead of a didactically responsible thread!
Anyway, the ensuing complications are highly undesirable for negation.