Help with 2 pulleys 2 objects.

[revolve]

Homework Statement

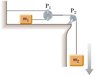
An object of mass on a frictionless horizontal table is connected to an object of mass m₂ through a very light pulley P₁ and a light fixed pulley P₂. (a) If a₁ and a₂ are the accelerations of m₁ and m₂, respectively, what is the relation between these accelerations? Express (b) the tensions in the strings and (c) the accelerations a₁ and a₂ in terms of the masses m₁ and m₂, and g.

Homework Equations

The Attempt at a Solution

I'm trying to setup the equations correctly. I know I need 2 equations for each object. Right?

Assuming positive direction is down:

$$\sum Fy = m_{2}g - T = ma_{2}$$

$$\sum Fx = T = ma_{1}$$

 

[kuruman]

There are two ropes in the system. In which rope is the tension T?

 

[revolve]

Okay the diagram was confusing. I thought it was all one rope.

Tension T would be related to P₂.

Not sure how I would proceed next.

 

[revolve]

$$\sum Fy = m_{2}g - T = ma_{2}$$

$$\sum Fx = T_{1}+T_{2} = ma_{1}$$

T₂ being the tension in P₁?

 

[PhanthomJay]

$$\sum Fy = m_{2}g - T = ma_{2}$$

$$\sum Fx = T_{1}+T_{2} = ma_{1}$$

T₂ being the tension in P₁?

Your equation in the x direction is incorrect. But before you go too far, you should first find the relationship between a1 and a2. If m2 drops down 1 meter, how far does m1 move in that same time period?

 

[revolve]

I'm not sure how to determine how far m₁ moves relative to m₂.

 

[PhanthomJay]

I'm not sure how to determine how far m₁ moves relative to m₂.

Try drawing a little sketch and note that the lengths of the ropes (the one on the right side of P1, and the continuous 'doubled up' rope on the left of P1), do not change in total length as the masses move. Start by assuming the length of the right rope is 2 m long (1 m to P1 to P2 and 1 meter P2 to m2), and assume that the length of the rope left of P1 is 2 m long (1 m from P1 to the wall, and 1 m from P1 to m1). Then use your visual imagination to see what happens if m2 were to nmov down 1 m from ints original position. It does take a close examination to determine this, it seems diffcult at first, but it's not too difficult once you see what's happening.

 

[revolve]

m1 moves half the distance of m2?

or the other way around. Confusing!

Okay P1 is half of P2 so m1 moves half the distance of m2. I think.

 

[PhanthomJay]

m1 moves half the distance of m2?

or the other way around. Confusing!

Okay P1 is half of P2 so m1 moves half the distance of m2. I think.

Indeed it is, revolve, it is indeed confusing. Look at it this way: Let the distance, initially, between P1 and P2 be 1 m, and let the distance between P2 and m2 be one meter, initially. Now if m2 were to move down by a meter, that would make P1 crash right into P2, correct? Such that now all the 2 m of rope we assumed, wrapped around P1 to the wall and m1, is now all on the top side of P1, 2 m from the wall. So where does that put m1??