Help with derivation of Malus' Law

[member 731016]

Homework Statement

Please see below

Relevant Equations

$I= I_{max}\cos^2\theta$ Where $\theta$ is the angle between the direction of propagation and axis of polarizer

I am trying to Derive Malus's Law. My textbook says that an electric field as an amplitude $E$ before passing thought the polarizer and reduce to $E_{trans} = E\cos\theta$.

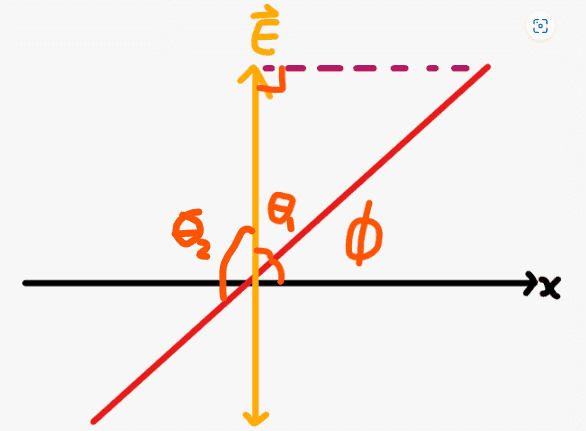
I am trying to understand why this occurs my considering a vertically polarized light passing though a polarizer that is at angle $\phi$ to the horizontal. The red line in the diagram below is the polarizer axis.

However, from the diagram, $\cos\theta = \frac{E}{E_{trans}}$ which rearranges to $E_{trans} = \frac{E}{\cos\theta}$ however, the component of the light transmitted should be $E_{trans} = E\cos\theta$. Could some please give me some guidance on what I have done wrong?

NOTE: $\theta$ could also be $\theta_2$ since $(\cos\theta_1)^2 = (\cos\theta_2)^2$

Many thanks!

 

[haruspex]

You chose to draw the dashed line horizontally, but you could have drawn it normal to the red line. How to decide?
$E_{trans}$ is the component of E parallel to the polarizer angle.

 

[member 731016]

You chose to draw the dashed line horizontally, but you could have drawn it normal to the red line. How to decide?
$E_{trans}$ is the component of E parallel to the polarizer angle.

Thank you for your reply @haruspex!

True, I can see how drawing the dashed line normal to the red line agrees with the textbook. However, deciding why is very interesting.

I recall from the dot product, that to find the component of one vector on another, we must find the projection of one vector on another and that method we do is to draw a line from one vector that is normal to the other vector.

Many thanks!

 

[BvU]

http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/polcross.html#c3

 

[member 731016]

http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/polcross.html#c3

Thank you for your reply @BvU!

Do you please know whether my dot product relation to find the electric field transmitted is correct? @haruspex you may also be interested in this algebraic derivation.

$\vec {E_{trans}} = \hat p \cdot \vec E$ where $\hat p$ is the unit vector that is pointing along the slit of the polarizer from the origin.
$|\vec {E_{trans}}| = |\hat p||\vec E|\cos\theta$
$|\vec {E_{trans}}| = |1||\vec E|\cos\theta$
$E_{trans} = E\cos\theta$

Many thanks!

 

[member 731016]

The textbook now says that the intensity of the wave is proportional to the amplitude squared.

Is it true that an EM wave is symmetrical in nature, so the amplitude is proportional to both the magnitude of the electric and magnetic field vector $I ∝ E^2 ∝ B^2$? Conversely, is it true that $|\vec E_{max}|= |\vec B_{max}|$?

Since we already have the magnitude of the transmitted electric field vector in terms of the magnitude of the initial electric field vector before passing though the polarizer, I think the choose the $I ∝ E^2$ relation.

So $I_{trans} = kE_{trans}^2 = kE^2\cos^2\theta$ and $I = kE^2$. Then we solve for the proportionally constant $k$ and set the two equations equal to get,

$\frac{I_{trans}}{E^2\cos^2\theta} = \frac{I}{E^2}$
$I_{trans}= I\cos^2\theta$

That is so cool!!

Many thanks!