Help with Frames Physics: Determining Reactions at A and E for Two 10-Inch Pipes

[jaredmt]

Homework Statement

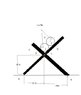
Two 10-inch diameter pipes (pipe 1 and pipe2) are supported every 10ft by a small frame like the one shown. Knowing that the combined weight per unit length of each pipe and its contents is 22 lb/ft and assuming frictionless surfaces, determine the components of the reactions at A and E.

Homework Equations

The Attempt at a Solution

first id like to make sure I am doing the weight of the pipe correctly:

Wboth = (22 lb/ft)(10ft) = 220lb. W1 = W2 = 110lbs

now that its all typed out i think i know what to do, but just correct me if I am wrong. i can get the vertical forces of A and E by finding the moment of the entire frame and setting it to 0. (the only forces involved are the weight of both pipes. A and E counter act it to make a moment of 0)
Then i can find all forces acting on Pipe 2, which is pipe 1, the pole and gravity pulling it down.
Then i find the forces acting on Pipe 1 which is pipe 2, both poles, and gravity.
Then i find the moment about the brown dot for each pole individually to find the horrizontal forces of A and Eedit: and also i believe the horizontal distance from the brown dot to where pipe 2 makes contact with the pole is 1.5rsin(theta)
the horizontal distance of pipe 1 is just rsin(theta).

 

[jaredmt]

ok nevermind, i just went through this problem and got the same answer they had in the book. its kind of annoying, that's like the 3rd problem this week where i figured it out as i was finished typing everything up and drawing the picture lol