How do I solve a Series RLC circuit?

[wiz0r]

Edited for assignment purposes...

 

[technician]

I think you need to know the frequency of the supply to get started... do you have it?

 

[wiz0r]

I think you need to know the frequency of the supply to get started... do you have it?

The source is just a DC source... so, there's no frequency.

 

[technician]

my apologies... I thought it was an AC circuit

 

[gneill]

Hi wiz0r,
Presumably the initial conditions that you're looking for is the state of the circuit at the time t=0⁺ when the switch has just opened.

Immediately before the switch opens, and assuming that the switch had been closed for "a long time", then your statement that the capacitor will look like an open circuit is correct -- no current will flow into or out of it. Similarly, the inductor will look like a short circuit.

Can you determine what voltage should be across the capacitor at t=0^-?

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

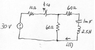
Assuming the switch is closed and the capacitor creates an open circuit... I'd have the source with the 10 and 60 ohm resistors... Using voltage divider I find that

Vc(0-) = Vc(0+) = 25.71 V, right?

That looks fine. So when the switch opens the capacitor will have that voltage on it as an initial condition. And the current will still be zero because of the inductor.

To find i(t) you'll have to either write and solve the differential equation for the new circuit configuration, or use a "canned" solution for the RLC circuit.

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

Alright.. sounds good.. I'll write what I have.. can you comment/guide me through it and point out any errors? Please...

Now as t = infinity...

i(inf) = 0... right? since the capacitor will act as an open circuit...

Now as for using KVL... after the initial differentiation of the KVL I get...

L d2i(t)/dt2 + R di(t)/dt + i(t)/C = 0

2.5 d2i(t)/dt2 + 120 di(t)/dt + i(t)/1m = 0

Now.. if I divide the equation by 2.5 I get..

d2i(t)/d2t + 48 di(t)/dt + 400 i(t) = 0

damping ratio = (48/2)/sqrt(400) = 1.2

since damping ratio > 1... circuit is overdamped...

s1 = -10.73
s2 = -37.26

i(t) = K1 e^(-10.73 t) + K2 e^(-37.26 t)

Ok... how about now? Any errors...??

It's looking good!

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

The equation should yield current values, and Vc(0) is a voltage.

At time t = 0 the current is zero, so K1 + K2 = 0. That is, K1 = -K2. You'll need to find another way to solve for the values. Perhaps if you could determine the initial rate of change of the current...

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

Okay.. btw, you meant that K1 = - K2.. right?

Right

so the initial rate of change of the current...

take the derivative of

i(t) = K1 e^(s1 * t) + K2 e^(s2 * t)

at t = 0.. gives

s1K1 + s2K2 = 0... which is what I had before and it was wrong... any other hint..?

s1K1 + s2K2 won't be zero. It'll equal the initial rate of change of the current. Go back to the circuit diagram and see if you can't determine what that might be. You've an inductor that has suddenly had a voltage Vc impressed upon it... how will it react?

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

The voltage of the inductor at t=0+ should be equal to:

VL(0+) = - Vc(0+) = -25.71, right?

Which implies that

di(0+)/dt = -25.71, Thus we can write that:

s1K1 + s2K2 = -25.71
K1 = -K2

K1 = -0.97 and K2 = 0.97, yes/no/maybe?

Sorry, I'm really tired.. >.<

The equation of interest for the inductor is its defining equation: V = L dI/dt. In this case there's an impressed voltage Vc across inductor L=2.5H. What's dI/dt?

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

dI/dt = Vc/L ?

dI/dt = 25.71/2.5 ?

dI/dt = 10.28?

Right. At t=0 dI/dt = Vc/L = 10.286 A/s. So, given K1 = -K2,...

 

[wiz0r]

Edited for assignment purposes...

 

[gneill]

and s1K1 + s2K2 = 10.286...

K1 = 0.388 and K2 = -0.388

Therefore...

i(t) = 0.388e^(-10.73 * t) + -0.388e^(-37.26 * t)

? =0

Looks good! Bravo!

 

[wiz0r]

Looks good! Bravo!

Woohoo... thank you so much!

One last thing... I'm told to make a plot of i(t).. to do that I used SPICE(attachment)... does the graph looks OK (attachment)?

@all other people: If anyone reading is taking the class with Rosado please say hi!

 

[gneill]

Looks okay. I think if you made the maximum timestep a bit smaller you might resolve the peak a bit better (eliminate the "flat bottom").

Here's the plot of the mathematical version:

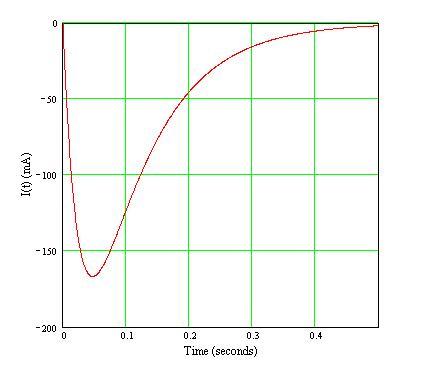
I've negated the current values ( -I(t) ) in order to match your Spice model current direction.

 

[wiz0r]

Looks okay. I think if you made the maximum timestep a bit smaller you might resolve the peak a bit better (eliminate the "flat bottom".

Here's the plot of the mathematical version:

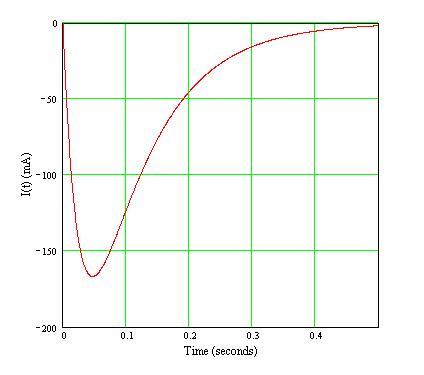
I've negated the current values ( -I(t) ) in order to match your Spice model current direction.

Perfect... thank you so much... I owe you big time... If I can repay you with something (except money.. I'm poor!) let me know! :)

 

[gneill]

Perfect... thank you so much... I owe you big time... If I can repay you with something (except money.. I'm poor!) let me know! :)

You're quite welcome. Just go get an "A" in your course!

 

[wiz0r]

You're quite welcome. Just go get an "A" in your course!

I will definitely try my best. :)

Thank you so much. Bye bye for now. :)

Edwin