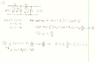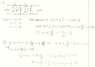Help with Signals and Systems Differential Equation Problem

[NHLspl09]

Hey guys, I was wondering if I could receive any help on a homework problem I have. I need to find the differential equation relating the input to the output. I've began working on it but feel like I've hit a brick wall in my work, any input?

Homework Statement

Attachment - Problem
Working on part c

Homework Equations

Attachment - Work

The Attempt at a Solution

Attachment - Work

 

[yongs90]

Take a look at my solution:
http://www.mypicx.com/09032011/Solution/

I leave the rearranging terms to you.. By the way how do you upload the picture like what is shown in this page. I don't know how to do it..

 

[vela]

You solved for i₁ in terms of i₂ and its derivatives. Now plug that into the other equation to eliminate i₁ completely and leave you with x(t) in terms of i₂ and its derivatives. Then since y(t) = L di₂/dt, you can write i₂ and its derivatives in terms of y(t).

 

[NHLspl09]

Take a look at my solution:
http://www.mypicx.com/09032011/Solution/

I leave the rearranging terms to you.. By the way how do you upload the picture like what is shown in this page. I don't know how to do it..

The thing is I need to do it using differential equations and not in the s domain. All I do to upload pictures is scan a document to paint then save it as a jpeg file and upload it using the manage attachments tool here.

You solved for i₁ in terms of i₂ and its derivatives. Now plug that into the other equation to eliminate i₁ completely and leave you with x(t) in terms of i₂ and its derivatives. Then since y(t) = L di₂/dt, you can write i₂ and its derivatives in terms of y(t).

Ok, I understand what you mean until you say to plug i1 into the other equation.. do you mean plug it into my x(dot) equation?? Where it is (i1-i2)?

 

[vela]

Yes, plug it into the x-dot equation anywhere i₁ appears.

 

[NHLspl09]

Yes, plug it into the x-dot equation anywhere i₁ appears.

I've done so and then solved for \frac{di1}{dt} in equation 3 and also plugged that into the x(dot) equation. Do I now take the derivative of this equation to leave it in terms of x?

 

[vela]

Equation 3 should be y(t)=L di₂/dt.

 

[NHLspl09]

Equation 3 should be y(t)=L di₂/dt.

If equation 3 is y(t)=L di₂/dt, then I'm not quite sure where it is plugged into in the other formulas

 

[NHLspl09]

I've been trying to restart the problem and look at it from a different approach but still no luck, any idea if I'm doing something wrong here? I've followed the same steps as taken in my notes from class and I can't seem to grasp this problem.

Edit: Any thoughts as to if I should be using KCL rather than KVL since I can't seem to figure this problem out?

 

[vela]

Your original loop equations were
\begin{align*}
x(t) - R_1 i_1 - \frac{1}{C}\int (i_1-i_2)\,dt &= 0 \\
\frac{1}{C}\int(i_2-i_1)\,dt - R_2 i_2 - L_1 \frac{di_2}{dt} &= 0
\end{align*}
(I think you had a sign error in the second equation.) The last term in the second equation is the voltage across the inductor, right? In other words, it's y(t). That's what your equation (3) should have been. I'm not sure why you used i₁ there instead. In fact, when you differentiated equation (2), you correctly expressed the derivatives of i₂ in terms of y(t).

You then differentiated each equation and got
\begin{align*}
\dot{x}(t) - R_1 \frac{di_1}{dt} - \frac{1}{C}(i_1-i_2) &= 0 \\
\frac{1}{C}(i_2-i_1) - R_2 \frac{di_2}{dt} - L_1 \frac{d^2i_2}{dt^2} &= 0
\end{align*}
You then solved the second equation for i₁ and obtainedi_1 = i_2 - R_2 C \frac{di_2}{dt} - L_1C \frac{d^2i_2}{dt^2}
Now just plug it into the first equation to get<br /> \dot{x}(t) - <br /> R_1 \frac{d}{dt} \left( i_2 - R_2 C \frac{di_2}{dt} - L_1C \frac{d^2i_2}{dt^2} \right) - <br /> \frac{1}{C} \left[ \left( i_2 - R_2 C \frac{di_2}{dt} - L_1C \frac{d^2i_2}{dt^2}\right) -i_2 \right] = 0
Note i₁ is gone. Now simplify it and then use the fact that y(t) = L di₂/dt to get rid of i₂.

 

[NHLspl09]

Note i₁ is gone. Now simplify it and then use the fact that y(t) = L di₂/dt to get rid of i₂.

Gotcha, my question is when you want to use y(t) = L di₂/dt how in the world can you manipulate this to get rid of i₂ throughout the xdot equation??

 

[vela]

The same way you did it before after you solved for i₁ after differentiating equation (2). What did you do back then?

 

[NHLspl09]

I ended up solving for a final answer of xdot = R1(\frac{y}{L1}+R2C\frac{ydot}{L1}+y(2dot)C)+(R2\frac{y}{L1}+ydot). Thank you guys for all of your help and input on this problem!

 

[vela]

Sorry, as you apparently realized, your original equations were right, and it was I who made the sign error in equation (2). So the loop equations are
\begin{align*}
\dot{x}(t) - R_1 \frac{di_1}{dt} - \frac{1}{C}(i_1-i_2) &= 0 \\
\frac{1}{C}(i_2-i_1) + R_2 \frac{di_2}{dt} + L_1 \frac{d^2i_2}{dt^2} &= 0
\end{align*}
which ultimately lead to the answer you found.

 

[NHLspl09]

Sorry, as you apparently realized, your original equations were right, and it was I who made the sign error in equation (2). So the loop equations are
\begin{align*}
\dot{x}(t) - R_1 \frac{di_1}{dt} - \frac{1}{C}(i_1-i_2) &= 0 \\
\frac{1}{C}(i_2-i_1) + R_2 \frac{di_2}{dt} + L_1 \frac{d^2i_2}{dt^2} &= 0
\end{align*}
which ultimately lead to the answer you found.

No problem at all! I figured it out last night with one of my friends in my course and figured I would post my final answer. Thank you very much for your help and input!