Plotting Length of Spring vs Load: Find Unloaded Length & Extension

AI Thread Summary
The discussion focuses on plotting the length of a spring against various loads to determine the unloaded length and extensions. Participants emphasize that the graph should be linear and caution against connecting the plot back to the origin, as the spring does not have a length of zero when no load is applied. There is confusion regarding the correct interpretation of the abscissa, which is clarified as the horizontal axis of the graph. A specific data point is identified as misaligned, suggesting that excluding it may yield more accurate results. The conversation highlights the importance of proper graphing techniques in analyzing spring behavior.
Taylor_1989
Messages
400
Reaction score
14

Homework Statement


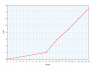
The following results were obtained when a spring was stretched:
Load/N: 1.0 3.0 4.5 6.0 7.5
Length of spring/cm:12.0 15.5 19.0 22.0 25.0

A) use the results to plot a graph of length of spring against load.
b) use the graph to find the:
i) unloaded length of spring
ii) extensions produced by a 7.0n load
iii) load required to increase the length of the spring by 5.0cm
 

Attachments

  • line_3BB501F6.png
    line_3BB501F6.png
    3.7 KB · Views: 632
Last edited by a moderator:
Physics news on Phys.org
I have used the graph that i created for the first question and get 10.2cm but the ans is 10cm so where i see a 1.8 difference of the graph the book i use sees a 2cm, so i can work out the other questions without doing the first can someone tell me where I am going wrong?
 
The plot should be linear. Your second point seems a little off. If you draw a line connecting points 1,3,4,5, it passes through 10 on the abyscissa.

Don't connect it back to 0,0 as you have done. It's length is not zero when the load is zero.
 
my maths is a little rusty could you please explain the abscissa, I can remember it has something to do with the x-axis for the carstine method ( I think ).
 
The abyscissa is the horizontal axis. You should not be drawing a line from (0,0) to
(12,1). Your data point at (15.5,3) does not line up with the others so if you forget about it and extrapolate the others to the abyscissa, you'll get what you seek.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Calculating the elastic potential energy from a force-extension investigation
Replies
16
Views
4K
Calculating the Spring Constant from Force-Extension Graph
Replies
6
Views
2K
Finding the force on a spring (Fs)?
Replies
2
Views
3K
Calculate persistence length from force extension data of a single DNA
Replies
2
Views
3K
MHB Find Extension of Springs: $\vec{r}$, $T$, and $x_E$
Replies
4
Views
2K
Finding Displacement on a Velocity Time Graph
Replies
4
Views
46K
Studying Skipping Chapters in Stewart’s Calculus? (Pearson's Edexcel IAL Background)
Replies
2
Views
193

Hot Threads

Recent Insights

Back
Top