NoctusPartem
- 1
- 0
- Homework Statement
- A proton is confined within an atomic nucleus of diameter 4.30 fm.
Estimate the smallest range of speeds you might find for a proton in the nucleus.
- Relevant Equations
- pL=hbar/2
My approach:
Assuming non-relativistic velocity:
$$p = mv$$
$$mvL = \frac{\bar{h}}{2}$$
$$v = \frac{\bar{h}}{2mL} = \frac{h}{4\pi mL}$$
$$v = (6.626*10^-34) / (4pi * 1.67*10^-27 * 4.3*10^-15)$$
$$v = 7.34*10^6 = .0245c$$
This answer is incorrect. What have I done wrong?
---
Edit: My lecturer's slides include the equation in the form:
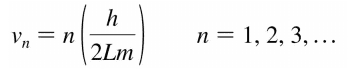
I'm not sure if or why this form should be used instead.
Assuming non-relativistic velocity:
$$p = mv$$
$$mvL = \frac{\bar{h}}{2}$$
$$v = \frac{\bar{h}}{2mL} = \frac{h}{4\pi mL}$$
$$v = (6.626*10^-34) / (4pi * 1.67*10^-27 * 4.3*10^-15)$$
$$v = 7.34*10^6 = .0245c$$
This answer is incorrect. What have I done wrong?
---
Edit: My lecturer's slides include the equation in the form:
I'm not sure if or why this form should be used instead.
Last edited: