How Can I Find the Coordinates of Rotated Points on a Stick?

[vonWolfehaus]

Homework Statement

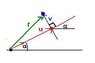
I need to find the x,y coordinates of the points that neighbor a center point that has been rotated around yet another point. An illustration is best:
http://coldconstructs.com/random/point_prob.png
Given: point of origin, angle, p1, p2
Needed: p1 a, b, c etc, p2 a, b, c, etc

Homework Equations

for p1/p2 I just do:
ax = cosine(angle)
ay = sine(angle)
new x = ax * distance from origin + origin x
new y = ay * distance from origin + origin y

The Attempt at a Solution

I thought I just add/subtract an amount somehow, somewhere? Tried, couldn't find the right stuff.

 

[ehild]

Think in vectors. See attachment. The position vector of a point is

\vec r=\vec u+\vec v

ehild

 

[vonWolfehaus]

Sorry, but I'm not a student so I don't remember what those lines above the letters mean :( You're talking to a philosophy degree turned web/game developer.

It looks like you're referring to the Pythagorean theorem, which doesn't work very well for this situation. I need to get to the new coordinates as cheaply (fast for the computer to crunch) as possible (I'm working on a game). Using angles and distances like that means a lot of unnecessary arctangent and square root operations, which are expensive.

Can't I just add/subtract some values and use the cos/sin I already have to determine the new coordinates?

I could add/subtract 90 degrees from the angle I have and do another sin/cos + distance but that seems like a waste. There has to be a cheaper way to do it...

 

[ehild]

Those letters mean vectors, which are given by their vertical and horizontal components. When you add two vectors, these components add up.
If the length of the vector u is u, (this is the distance of the midpoint of the stick on which your points sit) its horizontal component is u*cosθ, the vertical component is u*sinθ. If v is the position of a dot on the stick, the components of the v vector are
-vsinθ and vcosθ. You can assign a v value to each of your points. The position of a selected point is the vector r,sum of u and v, you get its components by adding up those of u and v:

The horizontal component is ucosθ-vsinθ, the vertical one is usinθ+vcosθ.

ehild