unscientific
- 1,728
- 13
Homework Statement
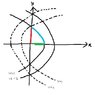
The question is attached in the picture.
The Attempt at a Solution
From the question I deduced that there are 3 boundaries: red, green and blue.
Blue Boundary
This one is the easiest:
That part of the curve of y2 = 4a(a-x), which corresponds to u = a.
Red Boundary
This corresponds to x = 0, y > 0.
When x = 0,
y2 = 4u2 = 4v2, which corresponds to u = v.
Blue Boundary
This happens when y = 0, x > 0.
When y = 0,
u = 0 or u = x. ------ (1)
v = 0 or v = -x.
Not sure what is going on here...
To try and vizualize the boundaries in the u-v (u,v) plane, I tried to find the intersection between each boundary.
Blue-red Intersection
u = a AND u = v
Therefore, this corresponds to the point (a, a)
I've yet to find the red-green intersection and the blue-green intersection..