How do I Calculate Normal and Applied Forces on a Branch Wheeled System?

[losbellos]

Dear Physics lover friends,

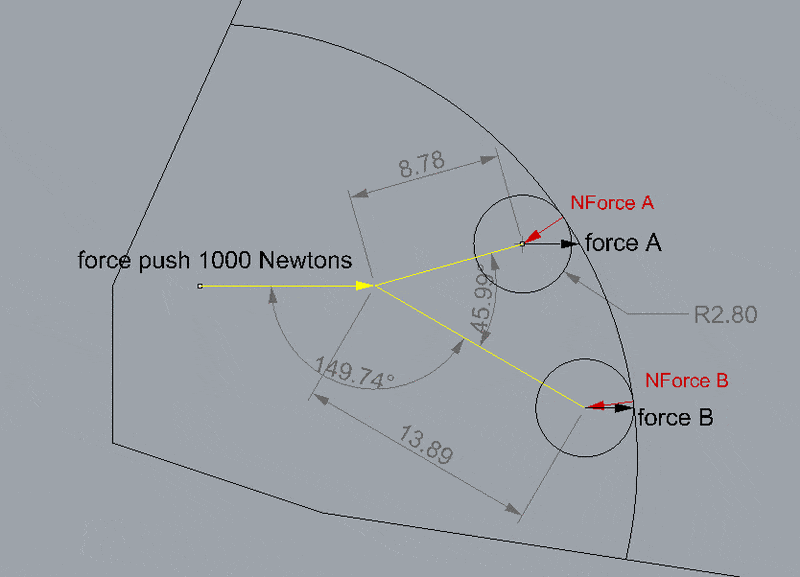
I am in the middle of something and I would like to ask a question on how to solve this branch wheeled problem.
The yellow lines are the branches, they have one wheels on them and the wheels are on a circular path.
I would like to know how much the normal force A and B and how much are the force A and force B.

Could you lease elaborate?
Thank you,

 

[CWatters]

Inspecting the drawing suggests that the three forces (1000N, NForceA and NForceB) can't sum to zero. For example the 1000N force is horizontal and both the NForces have downward vertical components. So either there is another force missing or the assembly must be accelerating. I might be wrong but I don't think you can solve it without more info.

 

[losbellos]

Hej, that might be that the system accels, but I believe that it is possible to zero it out, maybe by putting more wheels.
Actually on the end If I make sure the calculus is right I will try to convert it to a system that it will generate zeroed systems.

If I have only one arm that's easy I believe because the normal angle and the north angle can tell the normal components length (how much force it actually holds) and then the remaining force could generate some torque from the big circle's centerpoint (from the midponint not because there is no angle there)

So have you got any suggestions?

 

[CWatters]

The problem is I think you need to need to know it's mass in order to calculate the normal forces you asked about.

If you add more wheels I think you have a problem calculating how the load is shared between them. I think it depends on how the frame flexes. eg It becomes statically indeterminate.

 

[Dale]

I would set up a Lagrangian. Use 1000 times the horizontal position of the branch for your potential. Use an angular coordinate or two for the position of the wheels. Your KE is a function only of the derivative of the angular position. Then put in constraints for the arms and wall. Solve the Lagrangian and get your constraint forces.

 

[losbellos]

please can you be more specific? I mean please only answer if you know the answer.
This system must be able to solve by ratios and sin angles.

Thanks anyways!

[[Moderator's note: Per this request, the level of the thread has been changed from "A" to "B", and several off-topic posts discussing the appropriate level have been removed]]