Varaia
- 7
- 0
This one had three bullets by it so it's a pretty tough one.
Work and rambling thoughts so far... please tell me if I'm wrong.
This would be a change in entropy problem for the first couple of ratios right?
(delta)S=Sfinal-Sinitial=nRln(Vf/Vi)+nCvln(Tf/Ti)
yet it is an adiabatic operation so
pV^(1.3)=a constant during the adiabatic process
and since pV=nRT
TV^(1.3-1)= a constant
or TiVi^(1.3-1)=TfVf^(1.3-1)
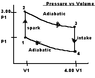
now in the picture there are two adiabatic processes one when the gas is expanding 2 to 3 so temperature is decreasing and one from 4 to 1 where the gas is being compressed and temperature is increasing so the ratio of
a) T2/T1 since there is no volume change= 3.00 (duh)
other ratio's I can see T3/T4=3.00,
P1V1=T1 3P1V1=T2 T1=1/3(T2) Still just not seeing how they get the other ratios
Question: What formula do I use to find out b,c,d, and e?
then I can do f.) on my own.
Numerical answers b)1.98 c)0.660 d)0.495 e)0.165 f)34%
The cycle in the picture (see attachment) represents the operation of a gasoline internal combustion engine. Assume the gasoline air intake mixture is an ideal gas with (gamma)=1.30. What are the ratios a) T2/T1 b)T3/T1 c)T4/T1 d)p3/p1 e)p4/p1 also f) what is the engine efficiency?
Work and rambling thoughts so far... please tell me if I'm wrong.
This would be a change in entropy problem for the first couple of ratios right?
(delta)S=Sfinal-Sinitial=nRln(Vf/Vi)+nCvln(Tf/Ti)
yet it is an adiabatic operation so
pV^(1.3)=a constant during the adiabatic process
and since pV=nRT
TV^(1.3-1)= a constant
or TiVi^(1.3-1)=TfVf^(1.3-1)
now in the picture there are two adiabatic processes one when the gas is expanding 2 to 3 so temperature is decreasing and one from 4 to 1 where the gas is being compressed and temperature is increasing so the ratio of
a) T2/T1 since there is no volume change= 3.00 (duh)
other ratio's I can see T3/T4=3.00,
P1V1=T1 3P1V1=T2 T1=1/3(T2) Still just not seeing how they get the other ratios
Question: What formula do I use to find out b,c,d, and e?
then I can do f.) on my own.
Numerical answers b)1.98 c)0.660 d)0.495 e)0.165 f)34%