Delta-One
- 5
- 0
I'm in a intro to circuits class for non-EE majors. One of the homework problems asks for the equivalent resistance.
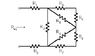
See the attached file for a picture of this system.
I know the first step is to add resistors R4 and R5 (in series) as well as add resistors R6 and R7 (in series). But after that I'm stuck. I think I have to apply a delta (triangle) to Y transformation but I'm not sure how to proceed with it. Any help would be greatly welcomed.
P.S. Please don't tell me the rules for series and parallel circuits. I know what the are I just don't know which resistors to combine in this example.
See the attached file for a picture of this system.
I know the first step is to add resistors R4 and R5 (in series) as well as add resistors R6 and R7 (in series). But after that I'm stuck. I think I have to apply a delta (triangle) to Y transformation but I'm not sure how to proceed with it. Any help would be greatly welcomed.
P.S. Please don't tell me the rules for series and parallel circuits. I know what the are I just don't know which resistors to combine in this example.