- #1
VitaminK
- 46
- 4
- Homework Statement
- Calculate the equivalent resistance. Is it possible to calculate an exact value?
- Relevant Equations
- Series: R1+R2+R3....Rn = Req
Parallel: (1/Req)=(1/R1)+(1/R2)…(1/Rn)
I start from far right:
Green and blue are parallel Connection:
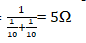
This in turn is in series connection with black resistor:
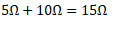
and so on ...

This is what I'm ending up with
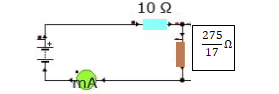
My final equivalent resistance is (275/17) Ω. Is this correct?
Green and blue are parallel Connection:
This in turn is in series connection with black resistor:
and so on ...
This is what I'm ending up with
My final equivalent resistance is (275/17) Ω. Is this correct?
