- #1
L_ucifer
- 12
- 0
New poster has been reminded to always show their work when starting schoolwork threads.
Summary: How do I solve the derivative of (((x^{x})^{x})^{x})...
How would I solve this derivative?
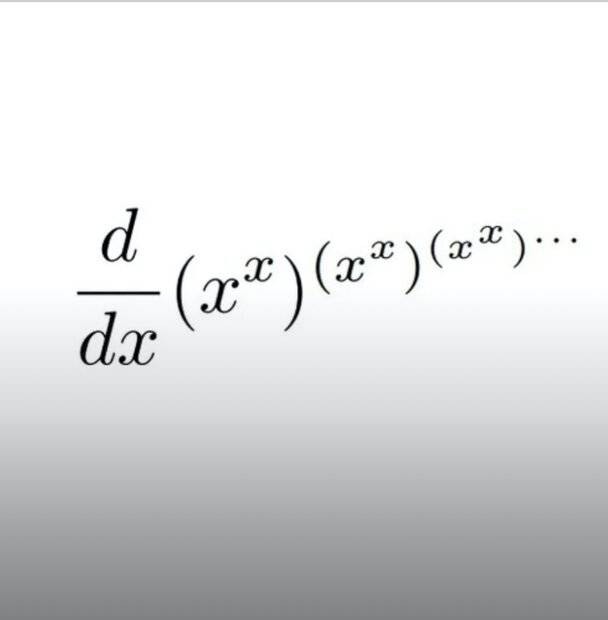
How would I solve this derivative?