How Do Projectiles Deviate in a Rotating Frame at 45°N Latitude?

[maxtor101]

Homework Statement

At apparent latitude 45◦N a shell is fired due North at an inclination of 45◦
to the horizontal with initial speed V . Show that, neglecting the curvature of the Earth, the shell will hit the ground at a point a distance \frac{2 \omega V^3}{3g' ^2}
East of the line of longitude through the point of firing. If the shell is fired due South under similar conditions, show that the deviation will be twice as great and to the West.

Homework Equations

I found the following equation in a mechanics book, it was derived from the rotating axes theorem:
<br /> \underline{r} (t) = \frac{1}{2}\underline{g}&#039;t^2 - \frac{1}{3} \underline{ \omega} \times \underline{g}&#039; t^3 - \underline{ \omega} \times \underline{V} t^2 + \underline{V}t<br />


Where \underline{r} (t) is the position vector of the particle at time t.
\underline{g}&#039; is the apparent gravity vector
\underline{ \omega} is the angular velocity vector of earth
\underline{V} is the velocity vector it is projected with.

The Attempt at a Solution

Well the position vector must be of the form

\underline{r} (t) = x(t) \underline{i} + y(t) \underline{j} +z(t) \underline{k}

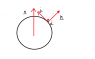
Where i,j,k are the unit vectors with the point of projection at the origin as shown in the diagram.

x(t) is the distance traveled north after t seconds.

Therefore x(t) = Vt cos45
x(t) = \frac{V}{\sqrt{2}} t

z(t) is the distance above the ground after t seconds.

z(t) = \frac{V}{\sqrt{2}} t - \frac{1}{2}g&#039;t^2

Solving for t when z(t) = 0 we get

t = \frac{V \sqrt{2}}{g&#039;}

This is the time when the particle hits the ground.

Now this is the part that I'm not sure of...

y(t) is the distance Earth rotates underneath the particle as it is in the air.

I'm not sure how to write down y(t)

I know that you find y(t) at t = \frac{V \sqrt{2}}{g&#039;}

I know it may be confusing but any help would be greatly appreciated guys and girls.

Thanks a mill in advance

Max

 

[maxtor101]

Sorry, forgot to upload diagram of the axes setup and stuff