How Do You Analyze Forces in a Non-Slipping Book Stack Scenario?

AI Thread Summary
In the scenario of analyzing forces in a non-slipping book stack, the top book (ma) is supported by the bottom book (mb) while both are accelerated to the right. The key forces at play include the applied force at a 64° angle, the normal force, friction, and gravitational force. Friction acts to prevent slipping and opposes the horizontal forces acting on the top book. The normal force is influenced by the vertical component of the applied force and the weight of the top book. Understanding these forces is essential for accurately drawing free body diagrams for each book.
nubshat
Messages
6
Reaction score
0
A hand supports two books, ma and mb, with ma on top. The hand accelerates the books p and to the right, with a pushing force directed 64° above horizontal. Assuming the upper book does not slip, draw a free body diagram for each book.

My attempt:
1NIx8Sk.png
 
Physics news on Phys.org
Which book is on top? and it would help if you defined all of your variables that you have shown.
 
ma is on top
R is the reaction force
n is the normal force
μn is friction
mg is gravity
|Fa| is the applied force
 
What force is friction opposing in order to keep it from slipping?

What is your normal force (or contact force)? Is it the same in this situation as it would be if the books were stationary?
 
Jesse H. said:
What force is friction opposing in order to keep it from slipping?

What is your normal force (or contact force)? Is it the same in this situation as it would be if the books were stationary?
I don't know that's the part I need help with
 
In this problem friction acts only in the x direction. What other forces do you have acting in x? What do you know about those forces if the book doesn't slip?

It might help to say that the reaction force is the force that the bottom book is pushing up on the top book. So the reaction force is actually the y component of your applied force!
 
Last edited:

Thread 'Rolling without slipping on a curved surface'

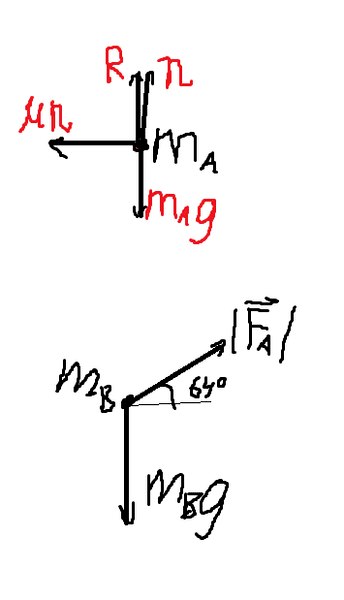
Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .
View full post »
Thread 'Voltmeter readings for this circuit with switches'

Thread 'Voltmeter readings for this circuit with switches'

TL;DR Summary: I would like to know the voltmeter readings on the two resistors separately in the picture in the following cases , When one of the keys is closed When both of them are opened (Knowing that the battery has negligible internal resistance) My thoughts for the first case , one of them must be 12 volt while the other is 0 The second case we'll I think both voltmeter readings should be 12 volt since they are both parallel to the battery and they involve the key within what the...
View full post »
Thread 'Trying to understand the logic behind adding vectors with an angle between them'

Thread 'Trying to understand the logic behind adding vectors with an angle between them'

My initial calculation was to subtract V1 from V2 to show that from the perspective of the second aircraft the first one is -300km/h. So i checked with ChatGPT and it said I cant just subtract them because I have an angle between them. So I dont understand the reasoning of it. Like why should a velocity be dependent on an angle? I was thinking about how it would look like if the planes where parallel to each other, and then how it look like if one is turning away and I dont see it. Since...
View full post »

Similar threads

Potential Mistake in Free-Body Diagram
Replies
5
Views
2K
Finding Radial Force from Free Body Diagram
Replies
4
Views
2K
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
Replies
41
Views
4K
Free body diagram on a block pushed against a ceiling
Replies
7
Views
3K
Statics free body diagram (frames and machines)
Replies
5
Views
4K
Forces and Free-Body Diagrams in Real-World Scenarios
Replies
5
Views
4K
Create the free-body diagram for the scenario below.
Replies
3
Views
2K
Analyzing Forces & Electrons: Free Body Diagram
Replies
2
Views
2K
Center of mass and momentum- A question about systems
Replies
25
Views
1K
Forces and Elevators: Free-Body Diagrams and Calculations
Replies
9
Views
6K

Hot Threads

Recent Insights

Back
Top