potato987
- 1
- 0
could anyone help me with this problem?
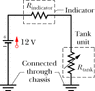
An automobile gasoline gauge is shown schematically in Figure 27-61. The indicator (on the dashboard) has a resistance of 10 . The tank unit is a float connected to a variable resistor whose resistance varies linearly with the volume of gasoline. The resistance is 200 when the tank is empty and 30 when the tank is full.
*Find the current when the tank is half-full*
V=IR
the current when the tank is empty is 12=I*200. so i multiplied that by two to get the answer but it was incorrect. i also tried to plug 15 into the equation since it's half of thirty but that too was wrong
Homework Statement
An automobile gasoline gauge is shown schematically in Figure 27-61. The indicator (on the dashboard) has a resistance of 10 . The tank unit is a float connected to a variable resistor whose resistance varies linearly with the volume of gasoline. The resistance is 200 when the tank is empty and 30 when the tank is full.
*Find the current when the tank is half-full*
Homework Equations
V=IR
The Attempt at a Solution
the current when the tank is empty is 12=I*200. so i multiplied that by two to get the answer but it was incorrect. i also tried to plug 15 into the equation since it's half of thirty but that too was wrong
Attachments
Last edited: