How Do You Calculate Norton's Current in a Complex Circuit?

[johnsy1312]

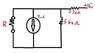
Find the Norton's equivalent for the following circuit attached







I have found the Norton's resistance:
RN=\frac{1}{1/5.6 + 1/2.2}=1.58k\Omega
I am confused on how to approach finding the current because of the +16v variable, what do i do with that variable? do i just treat that as any other voltage source? Is there another way i could draw that to make things more familiar?

 

[gneill]

The circuit doesn't show any ground (or common) connection, and so is just "floating" off the end of a supposed 16 V potential for which we have no reference point. No reference point makes the 16 V designation meaningless.

It also means there's no path from any part the circuit under study back to the "bottom" of the alleged 16 V source. What does that tell you about the current in that leg (the 2.2 K + 16 V leg) and its influence on the circuit?

 

[Simon Bridge]

Yah - the Norton equivalent is for a 2-terminal network.
This network only has one.

The problem statement does not even say which two points to take for the equivalent.

 

[gneill]

Yah - the Norton equivalent is for a 2-terminal network.
This network only has one.

The problem statement does not even say which two points to take for the equivalent.

Presumably the R between the two "terminal connection" circles is to be taken as the load, so as a stand-alone subcircuit a Norton equivalent is viable (and trivial!).

 

[Simon Bridge]

Hmm-hmmm... could also assume the bottom rail is ground.
This makes the voltage note as one end of a voltage supply.
Then it is not clear of the supply is to be part of the equivalent.

With nothing else to go on I'd ignore the voltage note to find the Norton.
Which does leave the R as the load yep.

 

[gneill]

Hmm-hmmm... could also assume the bottom rail is ground.
This makes the voltage note as one end of a voltage supply.
Then it is not clear of the supply is to be part of the equivalent.

I would disagree with being able to assume the shown bottom rail is ground. If you have labels for external sources then you must have labels for the common return. One without the other is not correct as the choice of which node to make common is actually arbitrary despite the temptation to make the assumption based on recognizing a familiar pattern in the drawing layout.

The only correct assumption one can make from the diagram as given is that the subcircuit is floating without a return path for the "16 V leg".

 

[Simon Bridge]

Yes, I agree that would be "correct" from the available data.
What is "correct" and what I would do are sometimes different things.
We need context for the diagram don't we?
Lets let OP fill in the gaps ;)