How Do You Calculate Oscillation Frequency for a Quadratic-Cubic Potential?

[Silviu]

Homework Statement

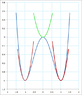
A particle moves in 1D in a potential of the form $$U=Ax^2+Bx^4$$ where A can be either positive or negative. Find the equilibrium points and the frequency of small oscillations.

Homework Equations

The Attempt at a Solution

So the equilibrium points are obtained by setting the derivative of U equal to 0. If A is positive the equilibrium point is 0 and the frequency is $\sqrt{2A/m}$. If A is negative the equilibrium points (stable equilibrium) are $\pm\sqrt{-A/2B}$. Now in the book, they say that the frequency of the oscillations here is equal to $\sqrt{-A/m}$ but I don't get this answer. This is what I did: $$\ddot{x}=-2Ax-4Bx^3$$ I will call the equilibrium point of the case when A is negative, simply $x$ and the small deviation $a$ so the equation becomes: $$\ddot{x}+\ddot{a}=-2A(x+a)-4B(x+a)^3$$ $$\ddot{x}+\ddot{a}=-2Ax-2Aa-4Bx^3(1+a/x)^3$$ $$\ddot{x}+\ddot{a}=-2Ax-2Aa-4Bx^3(1+3a/x)$$ and using the fact that x is the equilibrium point, we get: $$\ddot{a}=-2Aa-12aBx^2$$ and we know that here $x=\pm\sqrt{-A/2B}$ so we get $$\ddot{a}=-2Aa-12aB(-A/2B)$$ $$\ddot{a}=4Aa$$ so the osciallation frequency would be $\sqrt{-4A/m}$ (I ignored the mass in the equations). What am I doing wrong, why do I get that 4 there? Thank you!

 

[mjc123]

I agree with your answers; perhaps there is a mistake in the book.
(Strictly, what you have calculated is the angular frequency ω (rad/s). The frequency of oscillation (cycles/s) is ω/2π.)

 

[BvU]

Hi,

So you replace $U(x)$ by $U(a) = 2A a^2$

Who says you do anything wrong ? The factor 2 appearing in $U(a)$ makes it logical you get a factor $\sqrt 2$ in the frequency.

SO I suspect an error in the book answer...

The red parabolas (this is for ($A=-2,\ \ B= 1$) at $\pm 1$ are sharper than the green (for $A=+2,\ \ B= 0$) at 0