How Do You Calculate Tensile Load from Stress and Strain?

[a5hl3yi]

Question:

A beam is givn with an axial strain of 500x10^-6 and a Young's modulus of 200GNm^-2. work out the magnitude of the tenslie load.

Rlelvnt equations:

σ = YM x Axial strain

My workng:

So far I have worked out the stress of the beam to be:
36000000Nm^2
36MNm^2

But from here I don't know how to get the tensile load. Is there a formula I can use?

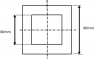
Picture of beam attached.

Thnx

 

[6Stang7]

Use dimensional analysis

 

[rock.freak667]

The same way you did it in the other thread.


$$stress=\frac{Force}{Area}$$

The tensile load is the force in the above formula.