lolcheelol
- 20
- 0
Homework Statement
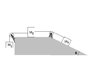
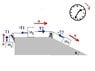
In the figure below, M1=1.00 kg, M2=2.00 kg and M3=4.00 kg. Theta is 30.0°. The pulley and all surfaces are frictionless. Find the tension in the two strings and the direction (entire system to the left/counterclockwise or entire system to the right/clockwise) and magnitude of the acceleration.
Diagram attached.
Homework Equations
F=ma
The Attempt at a Solution
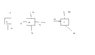
m1=A, m2=B, m3=C
I drew a free-body diagram for each of the blocks and I came up with these equations.
A=T1-W=ma
B=-T1-W+Fn+T2=ma
C=-T2-W+Fn=ma (I rotated it to have the block on a straight surface)
After doing these steps I am completely lost. I think I did my force equations correctly, but if someone can help me with this, step by step, it would be GREATLY appreciated.