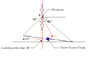
SUMMARY
The discussion focuses on calculating the tension in two chains (AB and CB) lifting a 5m long uniform beam AC with a mass of 600kg. The chains have lengths of 3m and 4m respectively, forming a right triangle configuration (3-4-5 triangle) when the beam is lifted. Participants suggest using the Law of Cosines to determine the angles and recommend creating a free body diagram at point B to analyze the forces and solve for the tensions in the chains. The center of mass of the beam should ideally align directly below point B when lifted.
PREREQUISITES
- Understanding of basic physics principles, particularly tension and equilibrium
- Familiarity with the Law of Cosines for angle calculations
- Ability to construct and interpret free body diagrams
- Knowledge of right triangle properties, specifically the 3-4-5 triangle
NEXT STEPS
- Study the Law of Cosines in detail for solving triangle-related problems
- Learn how to create and analyze free body diagrams in physics
- Explore the concept of center of mass and its implications in static equilibrium
- Review tension calculations in systems involving multiple forces and angles
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and statics, as well as engineers involved in structural analysis and design.