I How Do You Calculate the Dissolution Time of a Corroding Metal Sphere?

[johnsonb.engr]

Hello All

I could get some help I would greatly appreciate it.

I am trying to figure how to calculate the dissolution time of sphere undergoing constant corrosion at a rate
of corrosion.

Through a little google-fu, I found an article which gives me the solution ( http://arxiv.org/pdf/1208.5925.pdf )
but I am having trouble understanding the proof.

In this article there is a dissolving sphere

From this article we know that

the mass of the sphere is equal to dm/dt = -c*s(m) (1

and the general solution is

m(t)=mo - A*(mo^2/3)*t + (1/3)*(A^2)*(mo^(1/3))*(t^2) -1/27*(A^3)*(t^3)
or

m(t) = (a-k*t)^3
a = initial mass = (mo)^1/3
k = (A/3).

The article then gives an example where

mo = initial mass = 10 grams
p = density = 0.8 mg/mm^2
c = corrosion rate = -0.003 mg/(s*mm^2)

I am having difficulty understanding how to relate the rate of corrosion c to A.

I know that c = (dm/dt)/s(m)

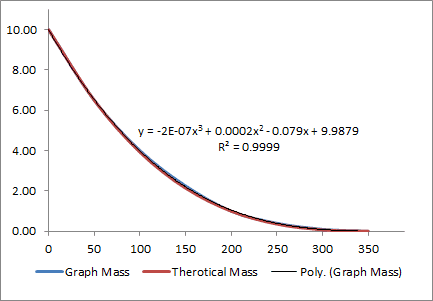
The article shows a series of graphs for Mass, Radius, SA, and Volume vs time.

I copied these graphs into excel and add used excel to find a trendline.

m(t) = -2E-07*t^3 + 0.0002*t^2 - 0.079t+ 9.9879

By plugging values into the trend line above I was able to find a solution to

A = 0.0173.

However, do not understand how to relate A to c(-0.003).

Some help would be greatly appreciated.

 

[Simon Bridge]

corrosion rate coefficient is given as a number c milligrams of mass dissolved per second from each square millimeter of surface area.
Therefore, an object with surface area A square millimeters will have an instantaneous rate of mass loss of $\dot m =cA$ milligrams per second.
You know how to find the surface area of a solid sphere from it's mass and density right?

 

[johnsonb.engr]

Hello Simon,

Thank you very much for your response.

Maybe I am not fully understanding your answer.

The A, I am trying to find is not the surface area of the sphere but rather a constant found in the solution to

dm/dt = -c*s(m) = -c*4πi*(3m/(4πi*ρ)^(2/3) (equation 1)

where the solution to the equation listed above is

m(t)=mo - A*(mo^2/3)*t + (1/3)*(A^2)*(mo^(1/3))*(t^2) -1/27*(A^3)*(t^3) (equation 2)

which simplifies to

m(t) = (mo^(1/3) - (A/3)t)^(1/3) (equation 3)

Where A is constant. Maybe I am wrong here, but I do not believe that A equation 2 and 3 is equal to the surfaces area of the sphere.

Am I wrong here?

If I am only given the density, rate of corrosion, and diameter of sphere, how would I go about finding equation 3.

Thank you very much for your help.

 

[Simon Bridge]

Then you need to identify what physical property the article is using the letter A to stand for. So far you have A=3k ... but that begs the question: what is k? (Though it is possible that A is just the constant of integration...)
Either that - or discard the article and work out your own solution.
The second is probably faster... I've already done it: took me a couple of minutes but then, I've had practise.