How Do You Calculate Total Impedance in a Tuned R-LC Circuit?

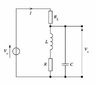
[bizuputyi]

Homework Statement

Given data of the given tuned R-LC circuit:

Q=1000
f_{resonance} = 1MHz
I = 15 \mu A
V_{s} = 2.5V
R_{L} = 10kΩ
C=2nF

Calculate the bandwidth, half-power frequencies, the value of R and L.
Estimate the impedance offered to the supply at resonance and at the frequencies of \pm2% from resonance.

Homework Equations

BW = \frac{f_{r}}{Q}

f_{lower}=f_{r} \Big( \sqrt{\frac{1}{4Q^2}+1}-\frac{1}{2Q} \Big)

f_{upper}=f_{r} \Big( \sqrt{\frac{1}{4Q^2}+1}+\frac{1}{2Q} \Big)

f_{r}=\frac{1}{2\Pi} \sqrt{\frac{1}{LC}}

Q=\frac{2\Pi f_{r}L}{R}

R_{dynamic}=RQ^2

\frac{Z}{R_{D}}=\frac{1}{1+j2Q\frac{δf}{f_{r}}}

The Attempt at a Solution

BW=1000Hz

f_{lower}=999.5kHz

f_{upper}=1000.5kHz

L=25.33 \mu A

R=0.159Ω

Do these calculations appear to be correct?

I'm struggling to find total impedance of the circuit, although I have some idea:

Is it simply Z=\frac{V_{s}}{I}=166.67kΩ?

or Y=j2\Pi f_{r}C+\frac{1}{R+j2\Pi f_{r}L} then Z=\frac{1}{Y}

from which I get Z=159006+j4780 Ω plus R_{L} total impedance comes to Z_{t}=169006+j4780 Ω

or from dynamic impedance equation Z=RQ^2=159kΩ plus R_L again Z_t=169kΩ

or this is a bit complicated but I found it in the textbook:
Z= \frac{R \Big( 1+\frac{(2\Pi f_r)^2L^2}{R^2} \Big) }{1+j(2\Pi f_r)\frac{L}{R} \Big( \frac{C}{L}R^2+(2\Pi f_r)LC-1 \Big) } from which I get Z=159138+j1700 Ω plus R_L again Z_t=169138+j1700Ω

Which of the total impedance is right? Maybe all of them are acceptable? Or a fifth one?

And as of to find total impedance at the frequencies \pm 2%:

From the relevant equation I've got Z=99-j3972Ω plus R_L → Z_t=10099-3872Ω

Your comments are greatly appreciated.

 

[rude man]

For high-Q circuits like this one you need to use approximations.

You should be able to derive the following:
|Z|/Zo ~ {1 + (2Qδ)²}^-1/2

where |Z| is magnitude of the RLC network impedance (as seen by R_L) at fractional freequency deviation δ, and Zo is the RLC network (real) impedance at resonance.

δ = (ω - ω_o)/ω_o
f = frequency, Hz
ω_o = resonant frequency
Q = quality factor at resonance.

You can then compute R and L for the RLC network and go on from there.

The sequence of computations might be ω_o → L → R → half-power δ → Z_o → |Z|_2%.

 

[bizuputyi]

Right, I think I get it. This is similar approach than mine and I get the same results. I was overthinking a bit on Z as such a high-Q circuit has a very sharp-edged graph.
That's one more tiny step towards my degree. Thank you!

 

[rude man]

Right, I think I get it. This is similar approach than mine and I get the same results. I was overthinking a bit on Z as such a high-Q circuit has a very sharp-edged graph.
That's one more tiny step towards my degree. Thank you!

Good luck to you!