How Do You Determine the Maximum Area of a Triangle in the First Quadrant?

[musicmar]

Homework Statement

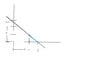
a. The area of a triangle is formed in the first quadrant by the x and y axes and a line through the point (2,1).
i. Write the area of the triangle as a function of x.
ii.Determine the domain of the function.
iii.Is there a maximum and minumum area for some value of x? If so, find the value analytically and graphically.

The Attempt at a Solution

I did part i and ii and only really need help with iii.
For i, I drew a graph of the first quadrant with a point at (2,1) and an arbitrary line through it and both axes. I have attached a graph from paint. I found the slope of the blue line (-1/x-2) and set it equal to the slope of the whole line (-y/x) in order to solve for y in terms of x. Because y= x/(x-2), the area of the triangle is:

A= 1/2 bh
=1/2 xy
= (x^2)/2(x-2)

ii. D: (2,infinity)

iii. I know there must be a maximum and minimum area as x approaches 2 and infinity, but I don't know how to "find the value analytically and graphically".

 

[gabbagabbahey]

Well, for local extrema, what can you say about dA/dx?... Is there anywhere else that global extrema may occur?

 

[njama]

Ok, you've done i) and ii) well.

Now, use
\begin{array}{l} (\sqrt{a} - \sqrt{b}) ^ 2 \geq 0 \\ \Rightarrow (\sqrt{a}) ^ 2 - 2\sqrt{a}\sqrt{b} + (\sqrt{b}) ^ 2 \geq 0 \\ \Rightarrow a - 2\sqrt{ab} + b \geq 0 \\ \Rightarrow a + b \geq 2 \sqrt{ab} \end{array}

But first...

A=\frac{x^2}{2(x-2)}

A=\frac{x^2-4+4}{2(x-2)}

Now, what can you do?