jamesd2008
- 63
- 0
Homework Statement
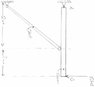
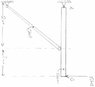
In the enclosed picture is a loaded beam and strut, what I need to do is determine the reactions at the supports. The problem is that I think the beam is indeterminable because there are more than three reactions?
Homework Equations
I do no the three equations of statics but don't no how to apply them in this context
The Attempt at a Solution
Could someone give me a hint in the right direction as to how to go about solving this problem?
Thanks in advance
James