Peter Jones
- 4
- 1
So in high school i studied the small oscillation of a simple pendulum with no air resistance. It reaches harmonic oscillation when the angle is small enough, so it is an approximation right? But what happens if the angle isn't small, will it still oscillate and how? According to energy conservation, it is supposed to. I came across this problem in a Mechanics book from Landau, and the result of cycle is a function of the amplitude of the oscillations. My question is that if this is still considered as a form of oscillation, what type is it?
Here's the picture of the problem from the book.
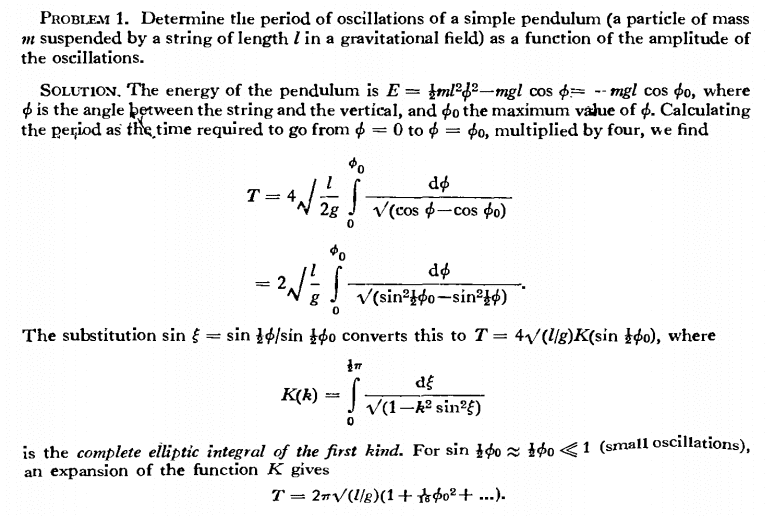
Here's the picture of the problem from the book.